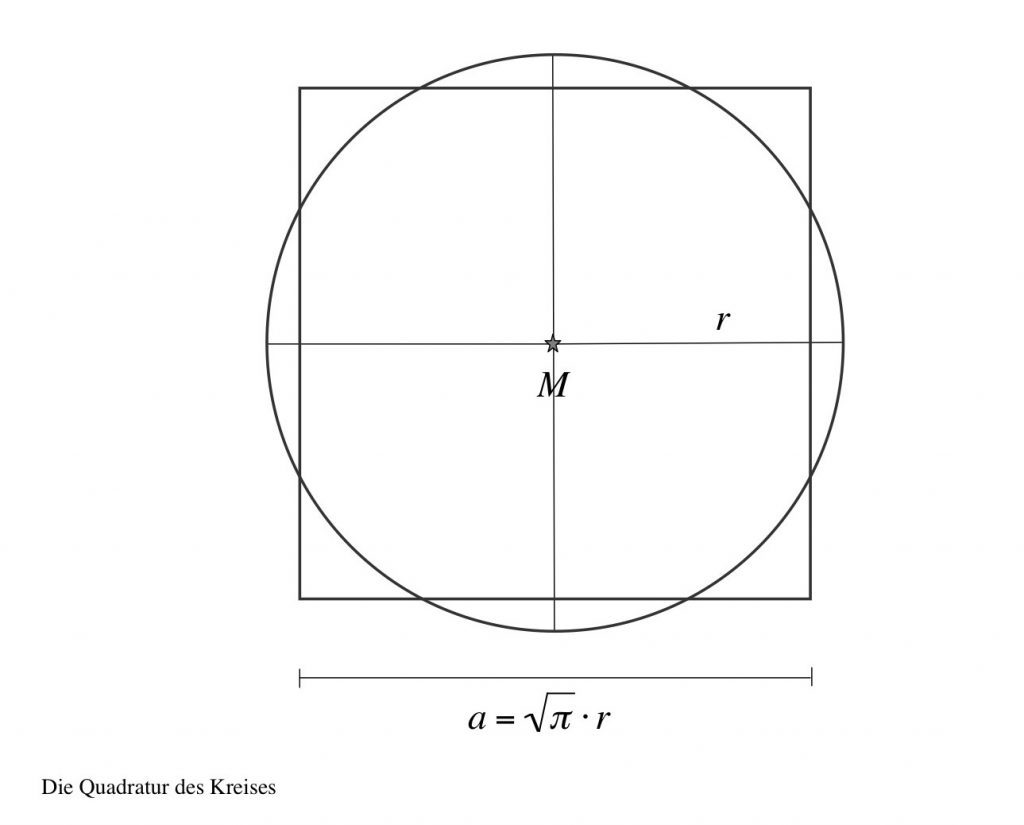
Die »Quadratur des Kreises« steht sprichwörtlich für ein unlösbares Problem – so ähnlich wie vielleicht „die Quellen des Nils suchen“ aus der Römerzeit (caput Nili quaerere) oder „einen Pudding an die Wand nageln“. Und? Handelt es sich hierbei in der Tat um ein „unlösbares Problem“ – oder liegt der Hase ganz woanders im Pfeffer?
Man nehme einen Kreis und mache sich bewußt, daß er über seinen Radius vollständig definiert ist: Ein gegebener Kreis kann sich von einem anderen Kreis allein über seinen Radius unterscheiden. Dann nehme man eben diesen Radius und multipliziere ihn mit einer ebenso handlichen wie eleganten Zahl wie der Wurzel aus Pi und schwupps – schon hat man die Seitenlänge des gesuchten Quadrates. Noch einfacher geht’s nicht.
Entfernt erinnert die Darstellung übrigens an eine auf das geometrisch unverzichtbare runtergebrochene Version von Leonardo da Vincis »Mensch«. Doch das nur am Rande.
Was hat es also mit der sprichwörtlichen Unlösbarkeit auf sich? Es sei nun mal, hört Bolle immer wieder, unmöglich, mit Zirkel und Lineal (also geometrisch) ein flächengleiches Quadrat zu konstruieren. Na und?, fragt Bolle. Ein Problem ist doch nicht schon deshalb „unmöglich“ zu lösen, weil es nicht mit jedem beliebigen Mittel zu lösen ist. So würde ja auch niemand auf die Idee kommen, einen Nagel mit einem Stück Emmentaler als Faustkeil-Ersatz in die Wand hauen zu wollen. Ist es deshalb „unmöglich“, einen Nagel in die Wand zu hauen? Natürlich nicht – zumindest solange man nicht versucht, damit einen Pudding an die Wand zu nageln. Was mit den Mitteln der Geometrie nicht geht, geht dann eben mit den Mitteln der Algebra. Wir erinnern uns: Kreativität ist die Kunst, nichtvorhandene Probleme zu ignorieren. Aber das ist ein anderes Kapitel.