Schlagwort: Mathematik

Veröffentlicht am

So 30-06-24 Die Wirklichkeit, die Wirklichkeit trägt wirklich ein Forellenkleid

Theorie und Empirie — nicht ohne Interpretation.

Hier zur Abwechslung mal wieder ein Beitrag aus Bolles Bildungsprogramm. Man kann sich ja nicht immer nur um den Unfug kümmern, mit dem die Polit-Apparatschiks dieser Welt meinen, selbige in einen besseren Ort verwandeln zu müssen.

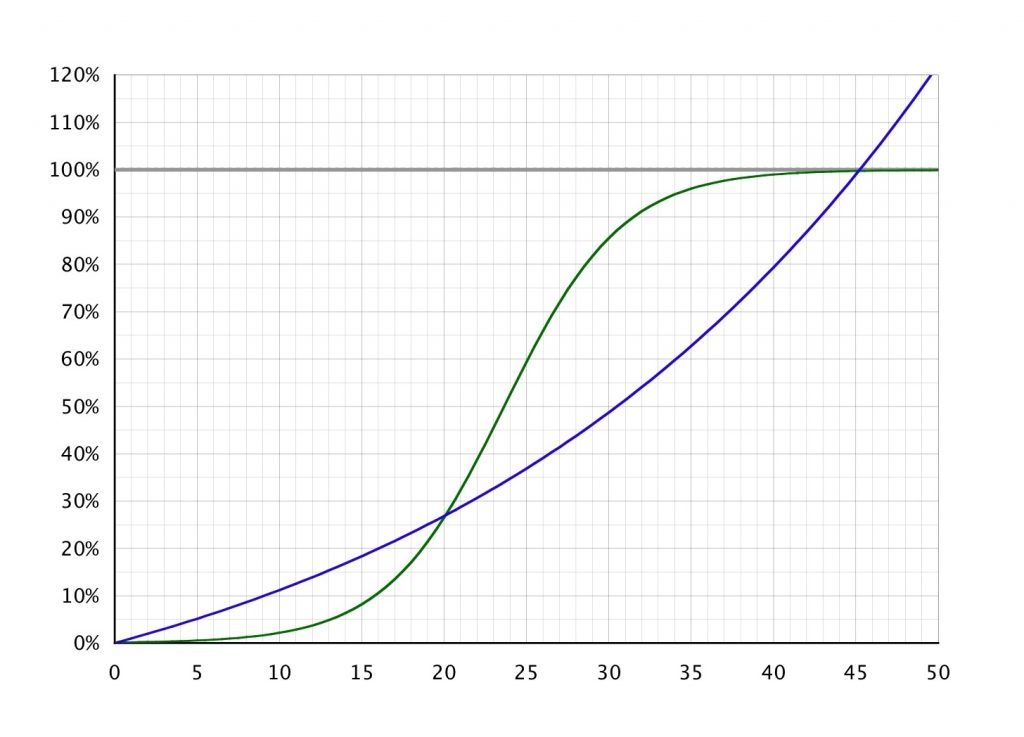
Keine Sorge. Wir müssen das Bildchen nicht völlig verstehen – vor allem nicht die Formel. Sie sagt einfach nur aus, daß die Masse eines Körpers mitnichten konstant ist, sondern daß sie mit der Geschwindigkeit, mit der der Körper sich bewegt, zunimmt. Das allein ist erstaunlich genug. Newton jedenfalls war das noch nicht klar. Demnach wäre jemand (beider- bzw. allerlei Geschlechts, of course), wenn er mit einem Affenzahn durch die Gegend düst, schwerer (i.S.v. massereicher) als wenn er nur bräsig im Liegestuhl läge. Allerdings – und da kommen wir schnell wieder auf den Boden der Alltagserfahrung – müßte sich derjenige schon mit 40% der Lichtgeschwindigkeit bewegen, um auch nur 10% schwerer zu werden (siehe das Pünktchen in der Graphik). Die meisten von uns werden ein solches Tempo allerdings kaum jemals erreichen, of course.

Aber von praktischen Erwägungen einmal ganz abgesehen. Hier soll es uns um die drei Hauptzutaten jeglicher Wissenschaft gehen. Da hätten wir als erstes die Empirie. Im Grunde handelt es sich dabei um ein Frage/Antwort-Spiel zwischen Welt I („alles, was der Fall ist“) und Welt II (die Welt der Wahrnehmung und Bewertung) mit der Erkenntnis der „Fakten“. Als nächstes hätten wir in Welt III (dem Weltbild, das einer für zutreffend hält) die Theorie als Destillat aus der Fülle der Fakten: So ist es nun mal! Ob das auch stimmt, wissen wir allerdings nicht. Zum Drei-Welten-Modell vgl. übrigens am besten So 26-05-24 Das bessere Argument.

Nun ist es so, daß der Zusammenhang zwischen Masse und Geschwindigkeit von Einstein schon 1905 in seinem Aufsatz ›Zur Elektrodynamik bewegter Körper‹ im Kern postuliert und seitdem auch tausendmal empirisch bestätigt wurde. Es ist also so!

Allein, was soll das bedeuten? Hier kommen wir zur dritten im Bunde, der Interpretation. Die Interpretation führt, wie’s scheint, ein geradezu stiefmütterliches Dasein in der Welt der Wissenschaften.

So geht die G’schicht, man könne leider, leider das Universum wegen der Gegebenheit Lichtgeschwindigkeit nicht so recht bereisen. Wenn nämlich ein Raumschiff sich der Lichtgeschwindigkeit nähere, dann – so die G’schicht – steigere sich dessen Masse ins Unendliche, und damit auch die zum Antrieb benötigte Energie. Unendlich viel Energie aufzubringen aber sei rein technisch nun mal unmöglich. Also auch Reisen in ferne Gefilde.

Soweit klingt das plausibel. Aber ist es auch wahr im weiteren Sinne? Ein Blick auf die Graphik zeigt uns – und hier sind wir bei der Interpretation von Empirie und Theorie –, daß wir ja mitnichten mit Lichtgeschwindigkeit fliegen müssen. Bei zum Beispiel „nur“ 87% Lichtgeschwindigkeit kommen wir gerade einmal auf die doppelte Masse (vgl. dazu wieder das Pünktchen in der Graphik). Das aber dürfte technisch ohne weiteres beherrschbar sein. Demnach würde eine Reise zu beispielsweise Proxima Centauri – dem nächsten Stern im Universum – nicht 4 Jahre und 3 Monate dauern, sondern eben 4 Jahre und 11 Monate. Bolle findet: die 8 Monate machen den Kohl dann auch nicht mehr fett.

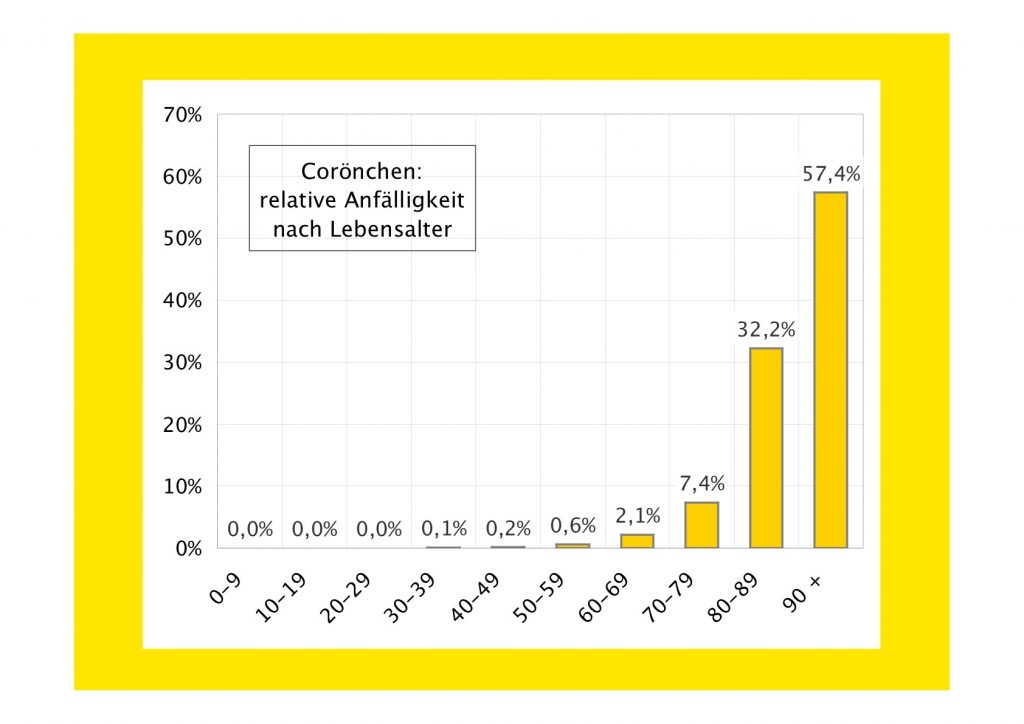
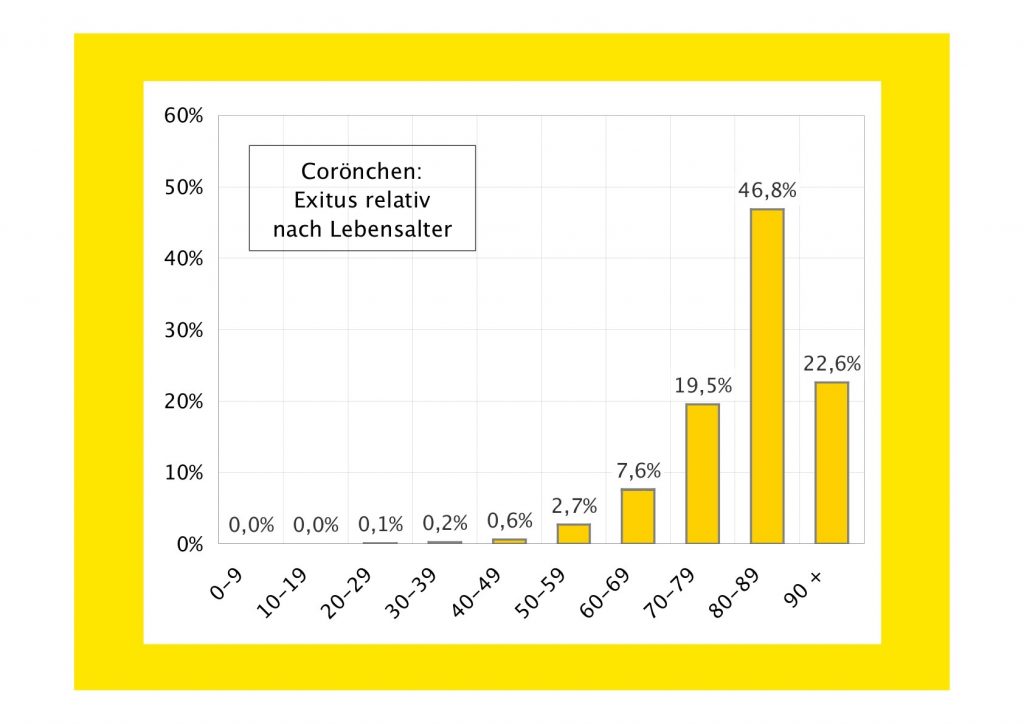
Das Problem ist also nicht die Unmöglichkeit, unendliche Energie aufzubringen, um ein bei Lichtgeschwindigkeit unendlich schweres Raumschiff anzutreiben. Das Problem ist vielmehr die Gegebenheit der Lichtgeschwindigkeit an sich. Das aber ist ein Unterschied, der einen Unterschied macht. Soweit also zur Interpretation gegebener „Fakten“ bei gegebenem theoretischem Schliff. Die Welt ist voll von derlei, übrigens: Corönchen, Ukraine, Klima … – you name it. Überall führen die nackten Fakten zu nichts als Verwirrung.

Bolle hat sich nach einigem Hin und Her übrigens entschlossen, den schlichten Begriff ›G’schicht‹ zu verwenden, wo andere von ›Erzählung‹ oder gar von ›Narrativ‹ fabulieren. Gemeint ist damit stets das gleiche: Ein Deutungsmuster aus der unübersichtlichen Fülle der Erscheinungen. Thomas S. Kuhn hat in seinem Werk ›Die Struktur wissenschaftlicher Revolutionen‹ dafür übrigens 1962 schon den Begriff ›Paradigma‹ verwendet. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

Veröffentlicht am

Di 14-12-21 Das vierzehnte Türchen …

Banal exponential.

Bolle hat jüngst erfahren, daß sich die Ansteckungen mit Corönchen in der Spielart ›Omikron‹ im Vereinigten Königreich (UK) alle zwei bis drei Tage verdoppeln würden – versehen mit dem Zusatz: „So etwas haben wir noch nie beobachtet.“ Natürlich hat Bolle nachgerechnet.

Wenn wir seriösen Schätzungen folgen und von aktuell 1.000 bis 2.000  Corönchen-Positiven ausgehen (auf die genaue Zahl kommt es überhaupt nicht an), dann würde es bei einer Verdopplungszeit von drei Tagen nur etwa 45 Tage dauern, bis auch der letzte Brite corönchen-positiv ist – mithin also schon Ende Januar! So schnell kann kein Politiker folgen – und selbst dem Journalismus 2.0 bliebe da glatt die Spucke weg.

Dabei sind mit ›Corönchen-Positiven‹ nach Bolles jüngster Definition Leute gemeint, bei denen aus medizinischer Sicht irgendwas nachweisbar ist – was aber weder mit Symptomatik noch mit Spreader-Potential auch nur das geringste zu tun haben muß. Bolle findet nämlich, daß an dieser Stelle allmählich etwas mehr Klarheit dringend geboten ist.

Betrachten wir unsere Graphik: Auf der Abszisse (x-Achse) findet sich die Zeit und auf der Ordinate (y-Achse) der Anteil der Positiven in Prozent. Dabei beschreibt die blaue Kurve eine „echte“ Exponentialfunktion, die wir den gegenwärtigen Verhältnissen im UK nachgebildet haben: Nach 45 Tagen sind wir demnach bei 100%. Ja, und dann? Da unmöglich mehr als 100% der Briten corönchen-positiv sein können, kann die Funktion so nicht stimmen. Corönchen vermehrt sich eben nicht exponentiell – jedenfalls nicht lange.

In Bronstein’s Taschenbuch der Mathematik – der Bibel der Mathematiker – heißt es dazu lakonisch:

Prozesse mit konstanter Wachstumsgeschwindigkeit
sprengen im Laufe der Zeit jede Schranke
und führen bereits nach relativ kurzer Zeit
zu einer Katastrophe.

Kurzum: Prozesse mit konstanter Wachstumsgeschwindigkeit (Prozesse, die Exponentialfunktionen folgen), haben in der Natur keinen Bestand. Sie haben eine ausgesprochene Neigung zur Selbstzerstörung – was Bronstein mit „Katastrophe“ umschreibt.

Was dann? Die Corönchen-Positivität folgt vielmehr der grünen Kurve. Dabei handelt es sich um eine von Bolle didaktisch geschmeidig angepaßte Sigmoid- bzw. Schwanenhalsfunktion. Das Ansteckungsgeschehen geht hier laangsam, gaanz langsam los, nimmt dann richtig Fahrt auf, um sich schließlich wieder zu beruhigen und der 100%-Grenze anzunähern. Mehr als 100% ist nämlich nicht zu schaffen – auch nicht für das mieseste und fieseste Corönchen.

Heißt das, wir können uns entspannen? Natürlich nicht. Schließlich erreicht auch die grüne Kurve die 100%-Marke, nur eben auf anderem Wege. So let’s go crazy: Warum steht in der Meldung „Verdoppelung alle zwei bis drei Tage“ – und nicht zum Beispiel: „Ende Januar sind alle Briten tot“ – und dann irgendwo im laufenden Text: „ … oder zumindest infiziert oder ganz zumindest corönchen-positiv“? Vielleicht noch versehen mit dem aufmunternden Spruch aus dem Anhalter durch die Galaxis: „Don’t panic“ – in großen, freundlichen Lettern, of course (vgl. dazu auch Do 03-12-20 Das dritte Türchen …). Das wäre doch viel zeitgemäßer und würde auch aufs feinste zu anderen Überschriften passen wie etwa: „Im Kampf gegen Omikron hoffen die Briten auf das zweite Impfwunder“. „Wunder“ – das klingt doch wirklich wunderbar weihnachtlich. Fehlt nur noch der „Impfzauber zur Heiligen Nacht“. Allerdings ist das dann doch schon wieder ein ganz anderes Kapitel …

Veröffentlicht am

Sa 04-12-21 Das vierte Türchen …

Very strange.

Immer wieder erweist es sich, daß es ausgerechnet die Künstler sind, die den meisten Weitblick an den Tag legen. Die Wissenschaften sind da weit, weit abgeschlagen. Aber übersetzen wir das erst mal:

Ein seltsames Spiel.
Die einzige Möglichkeit zu gewinnen
ist, nicht zu spielen.

Die Aussage stammt von WOPR. WOPR ist das Akronym für »War Operation Plan Response« – eine künstliche Intelligenz zur automatisierten Kriegsführung – und stammt aus dem Film WarGames (USA 1983 / Regie: John Badham). In dem Film geht es darum, daß sich das amerikanische Verteidigungsministerium entschlossen hatte, einen möglichen atomaren Gegenschlag einer Maschine zu überlassen, da sich Soldaten aus Fleisch und Blut als zu unzuverlässig erwiesen hatten. Nun war es so, daß WOPR zwar irriger-, dafür aber um so zuverlässigerweise auf atomaren Ernstfall erkannt hatte und nun im Interesse der gesamten Menschheit irgendwie gestoppt werden mußte – was bei einem vollautomatischen System ohne Not-Ausschalter nicht eben einfach ist. Gleichwohl gelang das den Helden in letzter Minute, indem sie WOPR in eine Partie Tic-Tac-Toe verstrickt hatten. Tic-Tac-Toe ist ein Brettspiel mit gerade mal 9 Feldern und nur gut 250.000 überhaupt möglichen Spielverläufen – für eine KI also höchst „überschaubar“, um nicht zu sagen: eine regelrechte Lachnummer. Das besondere daran ist, daß es mathematisch unmöglich ist zu gewinnen, solange der Gegner keinen Fehler macht – was WOPR nach wenigen Minuten helle war und zu besagtem Statement nebst Abbruch des atomaren Gegenschlages führte.

Was hat das mit uns zu tun? Nun, es ist eine schöne und darüber hinaus mathematisch unanfechtbare Allegorie auf menschliche Hybris – hier verstanden als den tiefsitzenden Widerwillen anzuerkennen, daß es manchmal Dinge gibt, die man leider nicht ändern kann – egal, wie sehr man sich das wünschen mag.

In der »Fibel zur Schreibwerkstatt«, einem in Entstehung begriffenen kleinen Vademecum für ambitionierte Autoren (beider- bzw. allerlei Geschlechts, of course) heißt es dazu:

Alles ist möglich? Denkste!
Laß Dir das bloß nicht einreden.

Zugegeben: Das Thema ist nicht wirklich weihnachtlich – dafür aber um so agnostisch-kontemplativer. Das aber ist dann doch schon wieder ein anderes Kapitel …

Veröffentlicht am

Do 02-12-21 Das zweite Türchen …

Denken schadet der Illusion.

Denken schadet der Illusion. Schöner hätte auch Bolle das nicht ausdrücken können. Fehlt nur noch der amtliche Hinweis: „Der Bundesbefundheitsminister mahnt“. Vielleicht sollten wir doch ernstlich erwägen, davon abzulassen, agnostisch-kontemplative Frühstückchen zu uns zu nehmen. Wer weiß, wer weiß …? Aber wir wollen das Kind nicht mit dem sprichwörtlichen Bade ausschütten. Erst hieß es: Laßt Euch impfen – dann wird alles gut. Wem das nicht gut genug war, dem ham se noch ne Bratwurst hinterhergeworfen. Dann hieß es: Laßt Euch auffrischen. Eins und eins, das macht zwei. Und überhaupt: „auffrischen“. Da waren wohl mal wieder exaltierte Sprachdesigner (beider- bzw. allerlei Geschlechts, of course) am Werk. Nach zwei kommt drei. Soweit können die meisten folgen. Auch hier wurde am schicken Wording nicht gespart: „Get your Booster, Baby“. Da die Ergebnisse aber weit hinter den Illusionen zurückgeblieben sind, müssen wir eben doch weiterdenken. Was passiert, wenn wir nicht nur bis drei zählen wollen? Vier …? Fünf …? Im Grunde ist es wie bei einem Adventskalender. Aber offenbar kommt so was in der Virologen-Ausbildung gar nicht vor. Pieks und denk’ nicht dabei. Das aber ist wohl doch schon wieder ein anderes Kapitel …

Veröffentlicht am

So 21-03-21 Die Entdeckung der Minderheit

Freiheit, die ich meine.

Solange es Menschen gibt, gibt es auch Entdeckungen. Denken wir nur zum Beispiel an das Feuer oder das Rad. Und schon wird es kompliziert. Das Feuer wurde ja nicht etwa „entdeckt“. Im Gegenteil: Es war schon immer da. Es wurde lediglich „gezähmt“ und in den Dienst menschlicher Bedürfnisse gestellt. Und auch das Rad macht erst dann Sinn, wenn man zusätzlich die Achse erfindet und einigermaßen befestigte Wege.

Ähnlich verworren verhält es sich mit jenen „Entdeckungen“, die bei Lichte betrachtet eigentlich eher Ideen sind, wie zum Beispiel Luthers „Freiheit eines Christenmenschen“ (1520) oder die grundlegende Idee der Französischen Revolution (1789), die in der Losung „Egalité, Liberté, Fraternité“ ihren knackigen Ausdruck fand. Die Übersetzung „Freiheit, Gleichheit, Brüderlichkeit“ meint das gleiche, klingt aber weniger musisch. Aber darauf soll es uns hier nicht ankommen.

Auch wollen wir nicht vertiefen, daß es bislang niemandem gelungen ist, auch nur einigermaßen bündig klarzulegen, was genau wir uns denn unter »Freiheit« vorzustellen haben. Thomas Hobbes (1588–1679) etwa hat darunter „das Fehlen jeglicher Bewegungsbehinderung“ verstanden, was Bertrand Russell (1872–1970) spöttisch als „wunderbar präzise Definition“ eingestuft hat. Das Problem: Wenn jeder (beider- bzw. allerlei Geschlechts, of course) auf „ungehinderte Bewegung“ bestehen würde, wäre absehbar Hauen und Stechen angesagt. Auch hauptamtlichen Denkern wie etwa Kant (1724–1804) oder Hegel (1770–1831) ist hierzu nicht allzuviel eingefallen – außer „Was Du nicht willst, das man Dir tu …“ (Kant) bzw. „Einsicht in die Notwendigkeit“ (Hegel) als begrenzendes Prinzip. Kurzum: Freiheit im Hobbes’schen Sinne mag zwar „wunderbar präzise“ definiert sein, ist aber leider praktisch völlig unbrauchbar. Warum?

Den ultimativen Grund liefert, einmal mehr, die Mathematik – genauer gesagt die formale Logik. Man nennt es dort Polylemma. Egal, was man macht: Man kann es nicht allen rechtmachen. Eines der bekanntesten Beispiele hierfür ist vielleicht die »Vater/Esel/Sohn«-Allegorie: Ein Vater ist mit seinem Sohn und einem frisch erworbenen Esel unterwegs. Anfangs gehen alle drei zu Fuß und werden von einem entgegenkommenden Wanderer ausgelacht: „Warum geht Ihr denn beide zu Fuß, so Ihr doch einen Esel habt zum reiten?“ Als dann der Vater aufsitzt, kommt der nächste Wanderer des Weges und bezichtigt den Vater der Kinderschänderei. Also läßt der Vater den Sohn aufsitzen – was von einem weiteren Wanderer dem Sohn als mangelnder Respekt vor dem Alter ausgelegt wird. Also sitzen beide auf – nur um sich den Vorwurf der Tierquälerei einzuhandeln. Schließlich nehmen die beiden ihre ganze Kraft zusammen und tragen den Esel nach Hause …

Kurzum: Wir haben es hier mit fünf Möglichkeiten zu tun, den Weg vom Markt nach Hause zurückzulegen – und keine davon bleibt unbekrittelt. Eine allgemein anerkannte Lösung (i.S.v. ›von allen anerkannt‹) ist nicht in Sicht. Game over.

Wir können das Thema an dieser Stelle nicht ausleuchten. Nur so viel: Die „Entdeckung der Minderheit“ führt mit mathematischer Notwendigkeit dazu, daß sich immer irgendwer in seinem höchstpersönlichen „Für-richtig-halten“ (im weiteren Sinne also in seiner „Freiheit“) eingeschränkt fühlen wird. Immer, immer, immer. Und – das kommt erschwerend hinzu: Je mehr Minderheiten wir als solche anerkennen, desto krasser wird es werden mit der gefühlten Einschränkung der Freiheit. Sind wir nicht letztlich alle „Andersdenkende“?

Schon aus diesem Grunde hält Bolle die Idee für noch nicht ganz zuende gedacht. Was dann? Begnügen wir uns an dieser Stelle mit einem Verweis auf Do 28-01-21 Sozialisation. Wird schon? Oder Hohn? Ansonsten ist das dann wohl doch schon wieder ein anderes Kapitel.

Veröffentlicht am

Mi 03-03-21 Wolle mer se eroilosse?

Wolle mer se eroilosse?

Seinerzeit schon, vor über 50 Jahren, hatte sich Pippi Langstrumpf im Namen der Ideosynkrasie souverän nicht nur über die Mathematik bzw. Arithmetik an sich, sondern sogar über deren Axiomatik hinweggesetzt. Damals war das noch spaßig und erfrischend. Allerdings dürfte kaum ein Schüler (beider- bzw. allerlei Geschlechts, of course) auf die Idee gekommen sein, das bei Pippi Langstrumpf gelernte im Rechenunterricht praktisch anzuwenden. Heute, 50 Jahre später, wird aus Spaß langsam Ernst. Wenn man den aktuellen Meldungen Glauben schenken darf, dann keimt in den USA, dem Land of the Free, allen Ernstes eine Debatte auf, die Pippi Langstrumpf locker in den Schatten stellt. Damit aber hätte der Ideosynkrasie-Virus eine Artengrenze übersprungen – vom Sozialen zum Formalen. Aber der Reihe nach.

Hier zunächst ein Beispiel für das Soziale: Wolfgang Thierse, der ehemalige Bundestagspräsident und SPD-Urgestein, hat neulich in einem Gastbeitrag in der FAZ beklagt, daß Debatten über Rassismus, Postkolonialismus und auch Gender-Sprech immer aggressiver geführt würden, und sich dabei über Cancel Culture eher kritisch geäußert. Auch sei Blackfacing nicht weiter bedenklich. Prompt zeigte man sich in der SPD-Spitze „beschämt“ über ein solch „rückwärtsgewandtes“ Bild, das so nicht länger zur Partei passen würde. Bolle meint: Woher wissen die eigentlich immer so genau, wo vorwärts und wo rückwärts ist? Und aus welcher Quelle speist sich eigentlich das Schamgefühl?

Hier nun das Formale. Anscheinend wird in den USA neuerdings ernstlich darüber debattiert, ob die Idee, daß  2 + 2 = 4 sei, nicht doch eher kulturelle Gründe habe, und nicht letztlich eine Folge von westlichem Imperialismus sei bzw. der Kolonisierung der Welt.

Dabei scheint sich die Virulenz bereits in einem fortgeschrittenem Stadium zu befinden: So heißt es in einem Rundbrief des Kultusministeriums (!) in Oregon, die Forderung an Mathematik-Schüler, in ihren Klausuren nur ein einziges, überdies auch noch möglichst zutreffendes Ergebnis vorzulegen, sei ein Zeichen „weißer Vorherrschaft“. Recht so, meint Bolle. Nieder mit den alten, weißen Männern und ihrer rassistischen Arithmetik – von Mathematik zu reden wäre hier wohl schwer übertrieben.

Bolle fragt sich ernstlich, ob er nicht vielleicht übertrieben stumpf ist bzw. zu wenig aufgeschlossen für neue Wege der Mathematik. Auch ist ihm klar, daß man eine Mathematik auch auf anderen Axiomensystemen aufbauen könnte. Weiterhin ist ihm allerdings auch klar, daß kein einziges dieser Axiomensysteme dazu führen würde, daß für ein und dieselbe Aufgabe mehrere „korrekte“ Lösungen möglich sind. Mehrere Lösungswege wohl – das aber ist hier offenkundig nicht gemeint. Und so kommt er nicht umhin, sich in Anspielung an einen running gag bestimmter Karnevalssessionen zu fragen, wer diese Leute reingelassen haben mag in die Uni oder ins Kultusministerium – und überdies ein Hygienekonzept zu fordern. Das aber ist vielleicht dann doch schon wieder ein anderes Kapitel.

Veröffentlicht am

Sa 30-01-21 Denken nützt …

Denken nützt.

Heute konnten wir in den bildungsbürgerlichen Medien erfahren, daß Statistiker ermittelt haben, daß die sogenannte „Übersterblichkeit“ in Deutschland zur Zeit bei 5% liegt – daß zur Zeit also 5% mehr Leute sterben als sonst. Kiek ma eener an, meint Bolle und verweist auf unseren Beitrag von neulich, Mo 25-01-21 Live forever? Dort hatten wir locker überschlagen, daß in Deutschland regelmäßig und sowieso Jahr für Jahr 1 Mio Leute sterben – wobei gegenwärtig etwa 50.000 Corönchen zugerechnet werden. Nun ist es so, daß 50.000 geteilt durch 1 Mio zufälligerweise justamente 5% ergibt. Dafür braucht man weiß Gott keine Statistiker – und erst recht keine Mathematiker. Das kann jeder Taschenrechner.

Natürlich möchte Bolle mitnichten „arrogant“ rüberkommen. Aber ein wenig verwundert ist er schon, mit welcher Gründlichkeit – um nicht zu sagen: Scheingenauigkeit – seit Monaten neben den regulären Nachrichten in ungezählten „Extras“ und „Spezials“ über R-Werte, Inzidenzwerte, Verstorbene, „Genesene“ und weiß der Teufel was sonst noch auf die Einerstelle genau (!) berichtet wird. Besonders pikant findet Bolle den regelmäßigen Hinweis, daß es sich hierbei nur um Datenmüll handeln kann (so sagt das natürlich keener – aber genau darauf läuft es hinaus), unter anderem, weil „am Wochenende weniger Daten gemeldet“ würden. Bolle meint: Wie man aus Daten schwankungsbereinigte Trends ermittelt, ist den Statistikern seit mindestens 100 Jahren klar. Warum dann das Volk Tag für Tag sinnlos zumüllen? Weil es „gefühlt“ mehr zu berichten gibt? Weil es die Leute in „gefühlter“ Dauer-Alarmbereitschaft hält? Wenn das mal gutgeht auf die Dauer … Aber das ist dann doch vielleicht schon wieder ein ganz anderes Kapitel.

Veröffentlicht am

Fr 29-01-21 Humor und Haltung

Humor und Haltung.

Ich war zu meiner Zeit ziemlich berühmt. Manche haben sogar meine Bücher gelesen. Diese Mischung aus Humor und Haltung bringen vorzugsweise Briten auf den Punkt. Zum besten gegeben hat das Stephen Hawking in einer von der BBC frisch ausgestrahlten Version vom »Anhalter durch die Galaxis«. (Ja, ja – der Dativ ist dem Genitiv sein Tod. Schon klar …). Das war am 8. März 2018 – sechs Tage vor Hawking’s Tod, by the way. Was soll man da sagen? Kult meets Kult, vielleicht. Der »Anhalter« selbst konnte 2018 seinen 40. Geburtstag feiern. And still going strong. Selbst Bolles Studenten haben eine zumindest vage Vorstellung davon.

Wie aber erlangt man eine solche Popularität? Und vor allem: Wie bringt man Leute dazu, sogar die Bücher zu lesen, die man schreibt? Hawking selbst soll im Vorwort seiner »Kurzen Geschichte der Zeit« angemerkt haben, daß ihn sein Verleger gewarnt habe: Jede Formel im Buch würde die Leserschaft glatt halbieren. Das muß vor 1988 gewesen sein. Allerdings hätte Hawking das wissen können. Schon 1951, also über 30 Jahre zuvor, hatte ein nicht weniger prominenter Kollege aus der OxCam-Connection, Bertrand Russell, in einer kleinen Ansprache zu »The Use of Books« die Befürchtung geäußert, daß zu viele Formeln wirklich zu viele abschrecken. Dabei ging es allerdings ausgerechnet um die »Principia Mathematica« (Russell / Whitehead 1910-1913). Aber Russell ahnte schon, was fehlt: Zu wenig „moral uplift“, also moralische Erbauung, im Standardwerk der Mathematik.

Und?, fragt sich Bolle. Was hat das mit mir zu tun? „Terror, Ficken, Hitler“ (so das Känguru in Marc-Uwe Klings einschlägigen Chroniken) einschließlich entsprechender Inhalte kann’s dann wohl ja auch nicht sein.

Das führt uns zu der Gretchenfrage für heute. Lesen Leute überhaupt noch? Oder sind sie vollauf damit beschäftigt, ihre Emails zu checken, Follower zu beglücken oder selber brav zu „folgen“ – oder auch nur die nächsthöhere Stufe in irgendeinem Daddel-Ding zu erklimmen? Das aber ist dann doch schon wieder ein anderes Kapitel.

Veröffentlicht am

Di 26-01-21 Live forever, again

Relative Corönchen-Anfälligkeit nach Lebensalter.

Nach unserem Beitrag von gestern (Mo 25-01-21 Live forever?) haben uns einige Rückmeldungen erreicht: Der wundersame Rückgang bei den über 90-jährigen könne ja wohl nur daran liegen, daß es von denen nicht mehr allzu viele gebe. Besten Dank dafür. Bolle – wie geht man mit so etwas um? Kein Problem – wir rechnen die Verteilung der verschiedenen Altersgruppen einfach raus. Gesagt, getan. Damit ergibt sich eine neue Graphik – die das Gemeinte allerdings nur noch unterstreicht.

In den Psaltern 90, 10 heißt es: Unser Leben währet siebzig Jahre, und wenn’s hoch kommt, so sind’s achtzig Jahre, und wenn’s köstlich gewesen ist, so ist es Mühe und Arbeit gewesen; denn es fähret schnell dahin, als flögen wir davon.

Das aber ist – man kann es kaum anders sagen – die conditio humana auf den Punkt gebracht. Kommen wir damit klar. Sagen wir so: Die Wahrscheinlichkeit, das nächste Jahr (oder die nächsten Jahre – darauf kommt es nicht an) zu überleben, sinkt mit zunehmendem Lebensalter. Und nichts anderes spiegelt sich in unserer Corönchen-Anfälligkeits-Statistik: Je älter, desto anfälliger fürs Ableben. Kann man unter diesen Umständen sagen, daß Corönchen ursächlich ist – oder ist es einfach nur auslösend? Ein Trigger, auf neudeutsch. Bolle vermutet letzteres.

Das aber legt einmal mehr nahe, daß Corönchen eher ein psychologisches Problem auf der Ebene „letzte Fragen“ ist und weniger ein medizinisches. Wir haben es hier und überhaupt mit einer Population zu tun, die mit ihren dringend anzuratenden agnostisch-kontemplativen Exerzitien schwer ins Hintertreffen geraten ist. Bedauerlich – aber auf die Schnelle kaum zu ändern. Philister – alles Philister. Das aber ist dann doch schon wieder ein anderes Kapitel.

Veröffentlicht am

Mo 25-01-21 Live forever?

Relativer Exitus nach Lebensalter.

Manche Dinge werden Bolle erst so richtig klar, wenn er eine Graphik vor Augen hat. Wenn die Angaben nicht lügen – wovon wir mangels besseren Wissens einmal ausgehen wollen – dann kann man Corönchen eigentlich nur als ›Rentnerproblem‹ einstufen. Nach entsprechender Datenverdichtung ergibt sich nämlich, daß 92,7% der Dahingeschiedenen auf Rentner entfallen. Das sind fast alle. Natürlich gönnt Bolle allen und jedem (beider- bzw. allerlei Geschlechts, of course) ein möglichst langes und auch möglichst erfülltes Leben. Indes: Macht bei dieser Datenlage die feine Unterscheidung zwischen „an Corönchen“ und „mit Corönchen“ überhaupt noch irgendeinen Sinn? Oder ist Corönchen nur ein, zugegeben: auffälliger, Auslöser für den finalen Exit, der uns Menschen als sterblichen Wesen nun einmal bestimmt ist? Ist nicht jede andere denkbare Sichtweise im Kern frevelhaft, hybrid – oder gar gottlos?

Bevor wir hysterisch werden – hier die frohe Botschaft. Aus der Tatsache, daß 92,7% der Dahingeschiedenen Rentner sind, folgt nicht, daß furchtbar viele Rentner dahingeschieden sind. Noch liegt die Sterblichkeit insgesamt bei lediglich 0,6‰. Das ist so gut wie Null. Nun könnte man dagegenhalten und argumentieren, daß sie damit absolut gesehen bei über 50.000 liegt – und das seien 50.000 zuviel. Wiederum umgekehrt sollten wir uns aber auch klarmachen, daß in einem Land mit einer Wohnbevölkerung von etwa 80 Millionen und einer Lebenserwartung von in etwa 80 Jahren natürlicher- bzw. auch statistischerweise ohnehin 1 Mio Einwohner pro Jahr das Zeitliche segnen. Das, so meint zumindest Bolle, relativiert die 50.000 doch sehr. Könnte es nicht vielleicht sein, daß wir es hier weniger mit einem medizinischen Problem und nicht doch eher mit einer Form von anthropozentrischem Totalitarismus zu tun haben? Frei nach dem Motto: Let’s live forever. Fuck the rest of all. Das aber ist dann doch schon wieder ein definitiv anderes Kapitel.