Mathematik

11-10-202611-10-2026

So 11-10-26 Millionen … und noch mehr

Kant, einer der Principes philosophicorum, der Fürsten seines Faches, meinte ja mal – und zwar an recht prominenter Stelle, nämlich in seiner ›Kritik der reinen Vernunft‹ (1781) –, daß Gedanken ohne Inhalt leer seien, und Anschauungen ohne Begriffe blind. Ja mei! Kant’ste das noch komplizierter sagen? In Bolles Frugalsprech heißt das schlicht und ergreifend: Es reicht nicht, nur zu fühlen. Man muß auch denken können. Allerdings auch umgekehrt, of course.

Eines der herrlichsten Beispiele für vorauseilendes Denken, dem das Fühlen kaum mehr folgen kann, ist wohl die Million/Milliarde-Konfusion. Wir hatten diesen Punkt schon einmal erwähnt. Allerdings war das vor furchtbar langer Zeit (Mo 09-11-20 Seid umschlungen Millionen!). Unsere Sonntagsfrühstückchen erreichen ja allmählich sowas wie historische Tiefe. Das dazugehörige Schildchen sah in etwa aus wie folgt – seinerzeit allerdings noch ohne Luftballöngers.

Halt! Stop! Bevor Ihr weiterlest: Wo in etwa würdet Ihr die Million „gefühlt“ verorten? — Und jetzt – aber erst jetzt – weiter im Text.

Die meisten Leute würden die Million bei etwa einem Drittel der Gesamtstrecke vermuten – also in etwa in dem Bereich, den wir mit den Pfeilchen angedeutet haben. Das ist, was das reine Denken angeht, natürlich etwas peinlich. Tatsächlich nämlich – also wenn man nachdenkt oder nachrechnet – liegt sie so ziemlich exakt auf dem Nullpünktchen. Warum das? Nun – eine Million ist der t a u s e n d s t e Teil von einer Milliarde. Eigentlich klar, das. Nehmen wir an, die Zahlenstrecke sei 10 cm lang. (Wie lang sie tatsächlich ist, hängt natürlich davon ab, ob Du das hier auf Deinem Handy liest oder auf einem Kingsize-Screen. Darauf kommt es für unsere Zwecke zum Glück aber nicht an). Nun ist ein Tausendstel von 10 cm aber eben nicht mehr als 0,1 mm – und paßt damit locker noch in das markierte Pünktchen.

Wie erklärt sich eine solch frappante Verwirrung des Gefühls? Nun, anthropogenetisch war es schlechterdings nicht wichtig, derlei zu wissen – und so haben wir als Menschheit das eben nie gelernt. Kein steinzeitlicher Jäger (beider- bzw. allerlei Geschlechts, of course) war je damit konfrontiert, sich vorzustellen, wie das wäre, wenn er es mit einer Million Säbelzahntigern zu tun hätte, oder einer Milliarde gar. Ein einziger war durchaus beeindruckend genug.

Heutzutage dagegen, wo wir als Menschheit in immer absurdere Größenordnungen vorgestoßen sind, kann es allerdings nicht schaden, sich des Unterschiedes endlich mal bewußt zu werden – auch wenn man ihn nicht „fühlen“ kann. 10⁶ … 10⁹ …? Soo krass kann der Unterschied ja wohl nicht sein. Denkste! Kann er wohl! Sagen wir so: Den Mathematikern ist es im Laufe der Jahrhunderte gelungen, aberwitzig große Zahlen gut gebändigt zu kriegen (Kant’sche Gedanken beziehungsweise Begriffe) – auch wenn das Gefühl (Kant’sche Inhalte beziehungsweise Anschauungen) schwer hinterherhinken mag. Wir erinnern uns: Der Durchmesser des beobachtbaren Universums beträgt gerade mal 10 hoch 27 (10²⁷) Meter (vgl. dazu So 26-07-26 Warum duzen Sie mich? Weil ich es kann!). Klingt gefühlt „überschaubar“ – ist aber doch ’ne ganze Menge.

Auf den Trick mit dem Pünktchen ist Bolle übrigens damals schon nicht hereingefallen. Bolle meint, daß läge wohl daran, daß er einen wirklich erstklassigen und voll old-fashioned Mathe- und Physiklehrer hatte, der auch zur Berechnung der kompliziertesten Zusammenhänge in diesem Universum nichts außer Rechenschieber hatte gelten lassen wollen. Von wegen Taschenrechner! Er war der Ansicht, das schärfe den Zahlensinn – und darauf komme es nun mal an, wenn man Mathematik betreiben wolle. Und so war es denn auch. Bolle und seine Oberstufen-Peers haben ihn geliebt. Sie wußten, was sie an ihm hatten: Hart zwar, aber hilfreich. Doch das nur am Rande.

Was Bolle aber wirklich schwer beeindruckt hat, war die Tabelle aus unserem heutigen Mathildchen. Wir haben die jeweiligen Zahlen in Sekunden ausgedrückt und (gerundet) in Minuten, Tage und Jahre umgerechnet. Damit entspricht der Unterschied zwischen einer Million und einer Milliarde dem Unterschied von 12 Tagen zu 32 Jahren (!). Bolle findet, das ist „gefühlt“ ein Unterschied, der durchaus einen Unterschied macht.

Unmittelbar lebenspraktisch wird das Ganze, wenn wir einen Blick auf die Possen der gegenwärtigen clique politique werfen.

Nehmen wir an, da verballert jemand bei einem informellen Sondierungsgespräch (beziehungsweise, wie es neuerdings auch gerne heißt, einem „Vor-Sondierungsgespräch“) mal eben 1.000 Euro. Das ist durchaus kein unrealistischer Wert. In einem der üblichen Edelschuppen, die man in diesen Kreisen vorzugsweise frequentiert, ist sowas schnell passiert – auf Spesen, versteht sich. Und stellen wir uns vor, das würde (siehe unser Mathildchen) 17 Minuten Deiner Lebensarbeitszeit entsprechen – denn schließlich bist Du es, der die Spesenrechnung letztlich zu bezahlen hat. Nun könnte man strikt pragmatisch-philosophisch sagen: Was soll’s? Mach ich doch gerne. Möglicherweise hast Du die ja sogar auch noch gewählt.

Stellen wir uns nun weiter vor, jemand verballert 1 Million – also zum Beispiel für die sprichwörtlichen Fahrradwege in Peru. Das würde schon 12 Tagen Deiner Lebensarbeitszeit entsprechen. Auch hier könnte man vielleicht noch sagen: Wieso? Was sind schon 12 Tage vor dem Herrn (beider- bzw. allerlei Geschlechts, of course)? Wenn’s doch der Völkerverständigung dient?

Stellen wir uns jetzt, drittens, vor, jemand verballerte 1 Milliarde, um „unsere“ – und damit vorgeblich auch Deine – Demokratie zu verteidigen. Das entspräche, um im Bild zu bleiben, immerhin satten 32 Jahren Deiner Lebensarbeitszeit. 32 Jahre aber entsprechen nicht weniger als zwei Dritteln Deiner gesamten beruflichen Existenz. Spätestens hier könnte der ein oder andere durchaus ins Grübeln geraten. Oder, im Kant’schen Sinne, das Denken schließt sich mit dem Fühlen kurz – ›fühlen‹ im Sinne von ›wirklich verstehen‹, statt nur zu rechnen. Und so soll es ja auch sein. Sentire aude, also – trau Dich, was zu merken. Das nämlich sollte – neben sapere aude (benutz’ Dein Gehirn), dem informellen Motto der Aufklärung – ja wohl das komplementäre Diktum sein. Zumindest dann, wenn wir von einer gewissen Konsistenz der kumulierten Kant’schen Konzepte ausgehen wollen. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

04-10-202604-10-2026

So 04-10-26 Erlesene Eliten

Reden wir mal wieder von Eliten. Das letzte mal hatten wir uns dieses Themas vor über einem Jahr angenommen (vgl. dazu So 27-07-25 Voll die Elite – oder doch eher Schiete?) Seinerzeit ist selbige – wie die Überschrift von damals schon erahnen läßt – nicht allzu gut davongekommen. Allein, es wird nicht besser, nur weil wir stille schweigen.

Wie w i r d man eigentlich Elite? Wenn wir von Standes- und Geldeliten einmal absehen wollen – hier reicht es durchaus aus, im richtigen Bettchen geboren zu sein – und uns auf Leistungseliten beschränken, dann geht das meistens nur auf die harte Tour – etwa so, wie Jacob Burckhardt (1818–1897) das beschrieben hat (siehe unser Schildchen). Ihm war durchaus klar, daß es sowas wie „ein festes Studium“ (Fachrichtung egal) braucht zu dem Zwecke, „konsequent arbeiten zu lernen“ und vor allem auch, „den nötigen Ernst in der Wissenschaft zu befestigen“.

Allerdings, das bliebe anzumerken, ist Bolle weit davon entfernt, unbedingt ein Studium voraussetzen zu wollen. Es gibt durchaus auch andere Wege, sich zu bilden. Sagen wir so: Ein malerischer Malermeister wäre Bolle durchaus lieber als einer, der akademisch in einem Master-Studiengang wie zum Beispiel ›John-Lennon-Studies‹ (soll es angeblich wirklich geben) brilliert hat. Auch sind durchaus Zweifel angebracht, ob derlei auch nur in die Nähe des Burckhardt’schen Ernstes in der Wissenschaft heranreichen würde. Damit soll natürlich nichts gegen John Lennon gesagt sein, of course.

Der Trick – wenn man das so nennen will – besteht darin, in die Top-Klasse vorzustoßen, also in die oberen knapp 2½ Prozent. Das ist natürlich nicht nach jedermanns Geschmack, of course. Auch übersteigt es mancher Menschen Fähigkeiten – was bei nur 2½ Prozent nicht weiter Wunder nehmen mag. Im Übrigen – doch das nur ganz am Rande – findet Bolle es immer wieder faszinierend, wie man mit einer handvoll an Mathildchen den gröbsten und dabei auch den größten Teil der Welt erklären kann. Auch scheint sich die an und für sich durchaus verständliche natürliche Reaktanz weiterer Kreise unserer geneigten Leserschaft – nicht zuletzt den Luftballöngern sei wohl Dank – erfreulicherweise durchaus in Grenzen zu halten.

Natürlich ist das alles ganz und gar nicht „inklusiv“. Im Gegenteil, es ist nachgerade e x klusiv. Man muß zu unterscheiden wissen. Und schon beginnt die Lebenslüge – der Haarriß im Gefüge. Seit es nämlich Mode geworden ist, jede Unterscheidung als „Diskriminierung“ zu diskriminieren, kann das gar nicht anders sein.

Nachdem das geklärt wäre: Wie b l e i b t man Elite? Neben der harten Tour gibt es noch sowas wie einen Hysteresis-Effekt. Hysteresis soll meinen, daß Ursache und Wirkung zeitlich auseinanderfallen. So muß einer in der Regel ziemlich lange ziemlich viel leisten (Ursache), bevor die Welt was merkt und einem eine privilegierte Position, einen Status, zuweist (Wirkung). Umgekehrt und ebenso gut kann es aber auch sein, daß einer schon lange nichts mehr leistet, ohne gleich seines Status enthoben zu werden: Man bleibt im Amt, obwohl man da, gemessen an der gegebenen Leistung, an sich rein gar nichts mehr zu suchen hätte. Featuring Wilhelm Buschs Julchen (1877) könnten wir, natürlich grob verkürzt, wie folgt formulieren:

Elite werden ist recht schwer,
Elite sein dann gar nicht mehr.

Einmal im Club – immer im Club. Auf Elite abonniert. Die Solidarität der Insider, der Eliten-Konsens, schützt einen und stützt einen. Bis es wirklich auffällt, daß man nichts mehr kann, ist man längst in Rente. Und nach mir die Sintflut.

Allerdings – das wollen wir nicht vergessen – neigt eine solche leistungsvergessene und nur noch aus idiosynkratischer Selbstherrlichkeit existierende Elite dann doch ein wenig zum Sklerotisieren. Man wird bräsig, faulig, läßt sich gehen. Bolle findet: ungut! und ist versucht, hierfür ein Wort wie Vulgär-Elite im Munde zu führen – was natürlich im Kern ein Widerspruch in sich ist. Um es einmal mehr mit Mephistopheles zu fassen: Spotten ihrer selbst und wissen nicht wie.

Allein, was wär’ die Wirklichkeit, wenn sie nicht so wirklich wär’? So wirklich – und auch noch so voll humorvoll. Das Universum schlägt gelegentlich zurück – und so kann ganz unversehens aus manchem Haarriß im Gefüge eine veritable Gletscherspalte werden.

So geschehen dieser Tage, als das Wort von den Vulgär-Demokraten die Runde gemacht hat – ein Begriff, der Bolle durchaus neu war. Aber wie gesagt: Das Universum hat Humor. Was genau damit gemeint ist? Wir wissen es nicht. Nur so viel:

Im Wesentlichen ging es wohl um Folgendes: Das Volk hatte sich erfrecht, zu wählen, was es will – und dabei den Korridor des Wählbaren verlassen. Kann es sowas geben? Aber Ja doch. Schließlich gibt es in „unserer“ Demokratie auch einen wohlgepflegten Korridor des Sagbaren. Warum dann nicht auch des Wählbaren? Doch damit nicht genug: In der Folge hatten die begünstigten Funktionäre – also die Vertreter dieses Teiles des Volkes – dann auch noch Ansprüche angemeldet. Im Extremfall wolle man sogar regieren. Das ist in der Tat vulgär. Das leuchtet Bolle ein.

Nehmen wir, da wir schon beim Thema sind, ›vulgär‹ als unmittelbares Antonym zu ›elitär‹. Das paßt auch schön zu unserem Mathildchen. Verstehen wir unter ›elitär‹ alles, was rechts von s = 2 ist, und unter ›vulgär‹ den ganzen groben, großen Rest, dann wird unmittelbar klar, daß eine Demokratie „vulgär“ sein m u ß – sonst wäre sie keine Demokratie. Das mag verwirrend klingen – ergibt sich aber rein mathematisch. Allein von daher muß es stimmen.

Nun aber prallen zwei Phänomene aufeinander. Wie gesagt – das Universum hat Humor. Auf der einen Seite die Vulgär-Demokraten, die alle Mathematik auf ihrer Seite haben. Auf der anderen Seite die – wie soll man sagen? – Elitär-Demokraten, also Leute, die im Zweifel zu Sachwaltern des Überkommenen verkommen sind. Hysteresis, halt. Unfähig, und vor allem auch unwillig, sich an i r g e n d etwas anzupassen. Demokratie? Gerne – doch störet unsre Kreise nicht. Im besten Ludewig’schen Sinne: L’État? Sind w i r – nicht etwa ihr (vgl. dazu So 18-01-26 L’État c’est moi oder Wir sind das Volk). I h r seid das Volk – und das soll nun mal nicht anmaßend sein. Man könnte hier – dem Lied der Deutschen folgend, wobei es wie immer keine Rolle spielen soll, ob wir musikalisch die Ost- oder die West-Hymne anlegen – glatt lyrisch werden. Hier Bolles Fassung:

🎶 Bräsig, bräsig woll’n wa bleiben
Woll’n wa bleiben allemal.
Zwar versperrt uns das die Zukunft
Ist uns aber auch egal. 🎶

Unter dem Strich sind das also Leute, die meinen, so eine Art gottesgnadentümliches Anrecht auf die Mitgliedschaft in der jeweils gegebenen Elite zu haben – einschließlich Dienstwagenschlüssel, of course. Will man von sowas regiert werden? Will man wohl eher nicht. Hinzu kommt eine pragmatische Frage: Wozu braucht einer einen Dienstwagenschlüssel, wenn er doch einen Chauffeur hat – oder derer gleich mehrere? (vgl. dazu nicht zuletzt unseren letzten Beitrag: So 27-09-26 Brötchentaste oder Ganz oben – wie geil!) Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

02-08-202605-08-2026

So 02-08-26 Einheit in Vielfalt? Oder EWA meets Mathe?

Oh weh, oh weh, oh jemine! Schon wieder ein Mathildchen – der dritten Observanz neben Schildchen und Bildchen. Bolle findet aber, das hier sei ja wohl noch harmlos. Und in der Tat zeigt es einen der schlichtesten Zusammenhänge, die überhaupt nur denkbar sind: Die Kurve hat die Form y = 1/x und stellt damit eine umgekehrte Proportionalität dar. Vornehm könnte man sie auch Hyperbel nennen – obwohl, das lenkt vom Thema ab. Immerhin konnten wir Bolle breitschlagen, die mathematische Strenge durch das Pfeilchen und drei Luftballöngers doch ein wenig abzumildern.

Direkte oder umgekehrte Proportionalitäten kennen wir alle aus den berüchtigten Dreisatz-Textaufgaben in der Mittelstufe: Ein kleines Päck Eier (6 Stück) braucht 6 Minuten, um al dente – oder sagt man à point? – zu sein. Wie lange braucht ein großes Päck mit 10 Eiern? Bolle hatte sich schon seinerzeit ganz köstlich amüsiert …

Die Kurve beschreibt den Zusammenhang zwischen Diversität und common sense: Geringe Diversität (beziehungsweise, was das gleiche ist, eine gewisse Homogenität) begünstigt ein hohes Maß an common sense (Punkt A), während, umgekehrt, ein hohes Maß an Diversität common sense doch eher erschwert (Punkt B). Wirklich verblüffend will Bolle das alles nicht scheinen. Dabei wollen wir unter ›common sense‹ nichts weiter verstehen als die von einer Gesellschaft überwiegend „geteilten“ Werte – wobei wir unter ›Werten‹ nichts sonderlich Hochtrabendes verstehen wollen, sondern lediglich ein ›allgemeines Für-richtig-halten‹.

Interessanterweise wird ›common sense‹ meist mit ›gesunder Menschenverstand‹ übersetzt. Bolle vermutet hier so eine Art imperialen Exzeß der Briten. Mit dem, was die Briten ›Menschenverstand‹ nennen, meinen sie wohl eher „Britenverstand“. Was Briten allgemein für richtig halten, muß noch lange nicht dem entsprechen, was zum Beispiel Sizilianer allgemein für richtig halten. Oder etwa Wüstensöhne (beider- bzw. allerlei Geschlechts, of course) – um das mal auf die Spitze zu treiben. Andere Länder, andere Sitten. Auch das will nicht weiter verblüffend erscheinen.

Kurzum: common sense ist eine unausgesprochene Übereinkunft darüber, was gesellschaftlich geht – und was nicht. Was man tut – und was nicht. Dabei folgt eine solche Übereinkunft – wie das in Bolles Kreisen heißt – einer sozialen Norm. Gleichzeitig – verwirrend genug – konstituiert sie aber auch die Norm. So etwas entwickelt sich – in Jahrzehnten oder gar Jahrhunderten. Und irgendwann ist es dann so. Alle halten es für richtig – und richten sich danach.

Sind Sizilianer oder Wüstensöhne – also Leute, die womöglich anderen Normen folgen – deshalb schlechtere Menschen? Natürlich nicht. Sie halten nur verschiedene Dinge für allgemein richtig. Auch kommt es überhaupt nicht darauf an, w a s man für richtig halten mag. Wichtig ist allein, d a ß sich alle – oder doch die meisten – zumindest einigermaßen einig sind. Das, was dabei rauskommt, nennt man dann eben ›common sense‹. Und zwar eben nicht im Sinne von ›gesunder Menschenverstand‹, sondern eher im Sinne von – wie soll man sagen? – ›gesunder Gruppenverstand‹. Ohne einen solchen Gruppenverstand kann eine Gruppe unmöglich existieren. Sie würde unversehens von ihren inneren kognitiven Fliehkräften in sprichwörtlich tausend Fetzen zerrissen werden. Nicht unbedingt unmittelbar – auf die Dauer aber schon.

Auch kommt es überhaupt nicht darauf an, daß alle genau das Gleiche meinen. Natürlich nicht. Darum sprechen wir ja auch von a l l g e m e i n e m Für-richtig-halten. Allgemein – und eben n i c h t en détail.

Nun ist es aber so, daß es sich bei Nationen um Gruppen handelt. Großgruppen, genauer gesagt. Eine Gruppe aber ist nichts weiter als eine ›Personenmehrheit mit Wir-Bewußtsein‹. Und dieses Wir-Bewußtsein entsteht bereits mit der Primärsozialisation – also schon im Kindesalter. Damit ist es – Entwicklungspsychologie, ick hör Dir trapsen – im besten Wortsinne irreversibel. Man könnte auch sagen: unkaputtbar. Es gibt nun mal ’ne Menge Dinge, die verdrahten sich im Hirn, lange bevor sich einer auch nur eine Vorstellung davon machen kann, was es mit ›verdrahten‹ auf sich haben könnte.

Die kesse Idee, man könne – 🎶 Freiheit, Freiheit, die ich meine 🎶 – in reiferen Jahren seine Hirnverdrahtungen mal eben ganz grundsätzlich umpolen, würde Bolle glatt ins Reich von Hülsenfrüchtchens Hirngespinsten verweisen wollen: Tolle Sache – funktioniert nur leider nicht. Wobei – das sei nicht unerwähnt – wir etwa einen 20-jährigen entwicklungspsychologisch durchaus und ohne weiteres als ›sich in reiferen Jahren befindlich‹ erachten können.

Wer es nicht glauben mag: Nehmen wir etwas vergleichsweise leicht Objektivierbares wie die Muttersprache. Was da verdrahtet wurde, sitzt. Von ein paar wenigen Super-Sprachgenies vielleicht mal abgesehen, ist es völlig unmöglich, eine zweite Sprache so zu erlernen und so zu beherrschen, wie das bei der Muttersprache (hoffentlich) der Fall ist.

Mit allen anderen Festverdrahtungen verhält es sich nicht anders. Die sitzen! Natürlich kann man in reiferen Jahren versuchen, sich dagegen aufzulehnen und das alles zu überwinden. Wie ging doch gleich der alte Sponti-Spruch? Wir wollen alles! Und das sofort! Allein es wird nichts nützen. ›Die Rechnung ohne die Realität machen‹ – wie das in Bolles Kreisen heißt.

Kurzum: je heterogener eine Gruppe – wir können auch sagen: je diverser –, desto Essig ist es mit dem common sense. Die einzigen, die das partout nicht einsehen wollen, sind nach Bolles Beobachtung die EWAs. Dabei steht ›EWA‹ für Eierlegende-Wollmilchsau-Apologeten, also Leute, die – wohl aus überschäumender Freiheitsmotivation heraus – der festen Ansicht sind, es müsse doch wohl möglich sein, alles gleichzeitig haben zu können, und das möglichst unbegrenzt (vergleiche den Pfeil in unserem Mathildchen). So zum Beispiel auch Einheit in Vielfalt – oder Freiheit in Sicherheit, oder was und wie auch immer. Für die Anerkennung umgekehrter Proportionalitäten bleibt da natürlich wenig Raum, of course. Und wohl auch nicht für Mathe überhaupt.

Dabei ließe sich an dieser Stelle unglaublich viel Energie sparen – was von gewissen Kreisen derzeit ja durchaus angestrebt wird. Warum? Weil, wenn etwas mathematisch nicht funktioniert, wird es auch im wirklichen Leben unmöglich funktionieren können – nicht einmal in einer möglicherweise besten aller möglichen Welten. Es lohnt sich also nicht, sich darum weiter zu bekümmern – ebensowenig, wie es zum Beispiel Sinn macht, etwa ein perpetuum mobile ersinnen zu wollen (um mal beim Energiesparen zu bleiben). Und so nennt man derlei Bestrebungen in Bolles Kreisen herzlich, und auch ohne jede Häme, kurz und knapp ›HH‹. „Haha“ für Hülsenfrüchtchens Hirngespinste. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

08-02-202609-02-2026

So 08-02-26 Könner versus Kasper (KvK)

Nichts läuft mehr richtig rund im Lande. Überall ist der sprichwörtliche Wurm drin. Zumindest k ö n n t e man das so sehen. In Bolles Kreisen spricht man hier auch keck von ›multiplem Systemversagen‹. Wenn aber etwas nicht so läuft, wie es soll, dann nennt man das nach alter Väter Sitte (beider- bzw. allerlei Geschlechts, of course) ein Problem. Dabei wollen wir unter ›Problem‹ nichts weiter verstehen als eine ›Soll/Ist-Diskrepanz mit momentaner Transformationsbarriere‹ (Bolle featuring Dietrich Dörner 1979) – wobei ›Transformationsbarriere‹ lediglich meint, daß nicht wirklich klar ist, wie man von einem unerwünschten Ist-Zustand in einen angestrebten Soll-Zustand kommen soll. Daran ändert sich übrigens auch dann nichts, wenn man das Problem – ebenso großspurig wie verhüllend, aber bitteschön – „Herausforderung“ heißt.

Wir hatten diesen Punkt vor knapp einem Jahr schon einmal aufgegriffen (vgl. So 16-03-25 Pferd verkehrt und Ritterehre oder Der super-duper Masterplan) und uns damals naheliegenderweise an Bolles Problemlösungszirkel (kurz ›PLZ‹) orientiert – einem Standardprocedere, das stets zur Lösung eines gegebenen Problems führt, oder aber zum Abbruch der Bestrebungen. Probleme nämlich, die man nicht lösen kann, sollte man tunlichst irgendwie loswerden. Komplizierter ist das alles nicht.

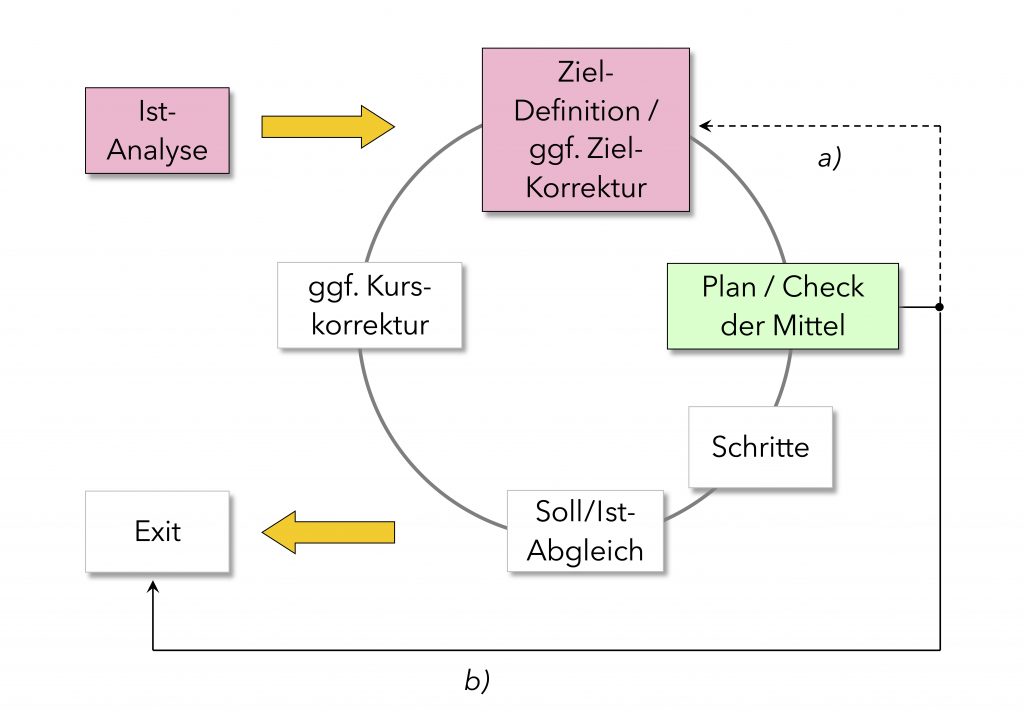
Der Problemlösungszirkel oder De arte solvendi.

Dumm nur, wenn man nicht weiß, wo man steht – und es womöglich auch lieber gar nicht so genau wissen will (Ist-Analyse), und (oder oder) einem auch gar nicht so recht klar ist, wo man eigentlich hinwill (Ziel-Definition) – von mehr Wohlstand, Freiheit, Demokratie beziehungsweise auch mehr Friede, Freude, Eierkuchen und dergleichen einmal abgesehen, of course. In Bolles Kreisen spricht man hier übrigens von ›nicht-wohldefinierten Zielen‹. Kein Wunder, daß Bolle dabei schon mal leicht unwohl werden kann.

Nun – in dieser Lage kann man als heillos überfordertes Hülsenfrüchtchen dann schon mal leicht auf die Idee verfallen, daß es doch zumindest nicht schaden könne, erst mal ganz viele Phantastilliarden ins System zu pumpen. Dann nämlich müsse es doch richtig rucken. Wäre ja gelacht! Bolle meinte damals schon: Denkste – muß es keineswegs! Und das hat es nach allem auch nicht – wie wir heute ziemlich sicher sagen können. Zwar sind die Phantastilliarden nicht wirklich weg. Sie sind nur anderswo – etwa auf den Forderungskonten sehr viel klügerer Paragonisten. Jedenfalls sind sie mitnichten da, wo sie ihre Wirkung entfalten sollten. Wie auch – bei d e m Plan? Und so wollen wir es Bolle auch nicht allzusehr verübeln, wenn er sich an dieser Stelle einmal mehr veranlaßt sieht, seine schönste Siehste!-Miene aufzusetzen – zumal er sich dabei ja stets stringent dezent zu halten pflegt.

Aber nehmen wir mal an – ebenso spaßeshalber wie kontrafaktisch –, soweit sei alles klar: Es existiere eine solide Ist-Analyse und auch ein wohldefiniertes Ziel. Da kann immer noch einiges dazwischenkommen auf dem Weg von Ist nach Soll. Bolle nennt es das KvK-Phänomen – wobei KvK für ›Könner versus Kasper‹ stehen soll. Dabei seien ›Könner‹ Leute, die wissen, was sie tun, und ›Kasper‹ – wie wir sie zärtlich nennen wollen – ganz entsprechend und tout au contraire Leute, die genau das eben n i c h t wissen.

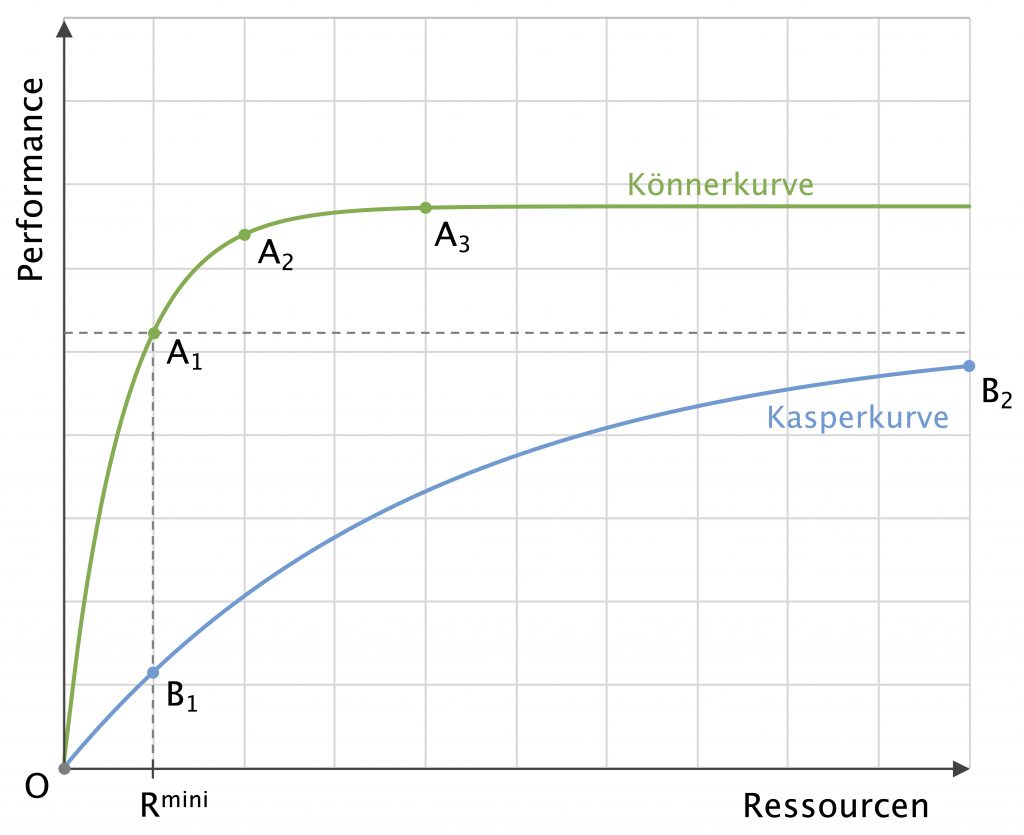
Unsere Graphik zeigt den Zusammenhang zwischen dem Einsatz von Ressourcen und der sich daraus ergebenden Performance. Dabei wollen wir unter ›Ressourcen‹ (oder schlicht ›Mitteln‹) das verstehen, was man von außen in Anspruch nehmen muß. ›Performance‹ stehe ganz allgemein für ›irgendwas gebacken kriegen‹. Das geht schon im Kleinsten los: Stellen wir uns zum Beispiel vor, wir wollten ein Regal anbringen. Ganz ohne Werkzeug (R = 0) wird das schwierig. Da wäre auch der pfiffigste Handwerker hilflos. Mit einer minimalen Ausrüstung aber (R^mini) – also Hammer, Bohrer, Schraubenzieher – läßt sich das Problem immerhin anpacken und auch leidlich zufriedenstellend lösen (A₁). Mit Bohrmaschine und Akkuschrauber geht‘s dann noch viel geschmeidiger (A₂und A₃) – w e n n man denn damit umgehen kann. Aber irgendwann – und zwar recht schnell schon – macht weiterer Mitteleinsatz keinen Sinn mehr: Der Könner hat alles, was er braucht, damit das Werk gelinge.

Anders verhält es sich mit der Kasperkurve. Ein minimaler Einsatz von Ressourcen (R^mini) führt hier zu wenig befriedigender Performance (vgl. A₁ zu B₁) – sei es, daß das Werk gar nicht gelingen will, sei es, daß es viel zu lange dauert. Eine Erhöhung des Mitteleinsatzes führt absehbar zu etwas besseren Ergebnissen – bleibt aber regelmäßig weit hinter der Könnerperformance zurück.

Fassen wir zusammen: Könner vermögen mit geringsten Mitteln Erstaunliches zu leisten. Kasper dagegen kriegen selbst mit erheblichen Mitteln nur wenig zustande. Aber sagt mal einem Kasper, daß er nun mal kein Könner sei. Er wird Euch hassen und bekämpfen! Besser werden seine Leistungen dadurch allerdings n i c h t . Da ist Regel #2 unseres Yoga-Tripletts vor (vgl. dazu So 01-02-26 Yoga für Agnostiker): Wirkung braucht nun mal Zeit. Und was Hänschen nicht gelernt hat, das lernt der Hans halt nimmermehr.

Genau das scheint Bolle übrigens auch der Grund zu sein, warum Nichts- beziehungsweise Wenigkönner – Kasper eben – dazu neigen, sich erstens immer gleich beleidigt zu fühlen, und zweitens, stets nach mehr und immer noch mehr Mitteln zu schreien. Kann man ja auch verstehen: Wer wollte schon gerne sein eigenes unabänderliches Nichts-Können beklagen, wenn er doch alles auf seine relative Mittellosigkeit schieben kann (vornehm: attribuieren)? Also müssen immer mehr Phantastilliarden her. Damit werde endlich alles gut.

Hier noch ein Fun-Fact am Rande: Die Kasperkurve konvergiert gegen die gestrichelte Linie. Das bedeutet, daß die Kasper dieser Welt mit einem (im mathematischen Sinne) buchstäblich unendlichen Mitteleinsatz gerade mal so viel gebacken kriegen wie ein Könner mit minimalen Mitteln (R^mini). Bolle meint, dann wäre das ja auch geklärt. Schaut Euch um auf dieser Welt. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

04-01-202604-01-2026

So 04-01-26 Wenn der Sekt nicht länger schreckt

Manchmal – nicht allzu oft, aber doch immer mal wieder – kommt Bolle sich vor wie ein Idiot. An und für sich ist das ja nicht weiter bedenklich, weil nur wirkliche Idioten sich niemals als solche fühlen. Aber gleichwohl: Was auf unserem Bildchen so unscheinbar aussieht – das eingekringelte Gläschen Sekt nämlich – hat eine längere Vorgeschichte. Zwar ist die Geschichte an sich nicht allzu lang – allein sie ist schon lange her.

Damals war Bolle in seinem Homeoffice – wie man das heute pseudoanglizistisch nennen würde – jeglicher Büromöbel abhold. Sowas kam ihm mitnichten ins Haus. Und so begab es sich, daß Bolles nigelnagelneuer Laptop (derlei gab es damals schon, wenn auch noch nicht weitverbreitet) auf Teppichhöhe residierte – und ein Gläschen Sekt in unmittelbarer Nachbarschaft.

Es kam, wie es kommen mußte: Schwupps, ein flotter Schwung aus dem Handgelenk – und das wohlgefüllte Gläschen Sekt befand sich stante pede in der Horizontalen. Zwar hatte das Glas an sich den Positionswechsel bestens überstanden – allein der Sekt wollte mit des Rechners Innenleben nicht wirklich harmonieren. Futschikado! Rien n‘allait plus! Und so war unvermittelt Schluß mit Homeoffice in jener Nacht. Genügend Sekt war aber noch da. Ein Glück! Auch wollte der Computerhändler den Laptop umgehend und kostenfrei durch einen neuen ersetzen. Schließlich – doch das nur am Rande – war die Firma, für die Bolle seinerzeit als Chefeinkäufer tätig war, ein Premium-Kunde. Bis auf 100 ml vergossenen Sektes war also nichts passiert.

Gleichwohl fühlte Bolle sich veranlaßt, den Vorfall zu evaluieren: (1) Sekt schmeckt – das sowieso. (2) Sekt schreckt – zumindest, was sensible Maschinchen angeht. Als unmittelbare praktische Konsequenz gab es seitdem bei Bolle Sekt nur noch aus Senfgläsern – natürlich sehr formschönen Senfgläsern, of course. Zwar waren die nicht ganz so dünnwandig, und auch nicht so edel – dafür aber waren sie ausgesprochen standfest. Bolle hatte damals eigens eine mittlere Menge Senf minderer Güte gekauft und in den Abfluß gespült – nur um die Gläser zu haben. Und so war es bis vor wenigen Tagen geblieben.

Die Senf-Sektgläser hat Bolle übrigens heute noch ohne jeden wie auch immer gearteten Abgang. Bei entsprechend pfleglicher Behandlung (keine Spülmaschine, stets einigermaßen aufgeräumte Küche, etc. pp.) haben sie sich als quasi unkaputtbar erwiesen. Die Sektflöten von damals – also die, die Bolle wirklich mag (vgl. dazu Do 04-12-25 Das vierte Türchen: Tempi passati) haben sich umständehalber neulich auch wieder eingefunden. Warum also nicht das Funktionale mit dem Ästhetischen verbinden? Und so kommt es, daß Bolle sich für seinen Sekt eigens einen Logenplatz ausgedacht hat – in Armeslänge zum Küchenstuhl (der Bolle als Arbeitsplatz dient) und trotzdem technisch himmelweit entfernt von sämtlichen sensiblen Gerätschaften. Da sollte eigentlich nichts mehr passieren dürfen.

Allein Bolle wäre nicht Bolle, wenn er der Sache nicht mathematisch auf den Grund gegangen wäre: Und so kam es denn heraus, daß bei den Sektflöten ein Neigungswinkel von gerade mal 15° (gerechnet in üblichen Altgrad mit 360° als Vollwinkel) ausreicht – und das Glas liegt auf der Nas‘. Und das bei einem Schwerpunkt, der sich in so luftigen Gefilden wie zwei Dritteln der Glaseshöhe – zumindest aber der Füllstandshöhe – befindet. Zum Winkel stelle man sich ein Tortenstück vor, das nach alter Väter Sitte (beider- bzw. allerlei Geschlechts, of course) ein Zwölftel einer Torte ausmacht, und das dann noch einmal halbiert. 15° sind also wirklich nicht viel – und so ist es gar nicht schwör mit dem Malheur. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

18-12-202518-12-2025

Do 18-12-25 Das achtzehnte Türchen: Mathematik ohne Sinn ist hohl

Kant – der Kant, of course – meinte in seiner ›Kritik der reinen Vernunft‹ (1781/1787), daß Gedanken ohne Inhalt ja wohl leer seien und Anschauungen ohne Begriffe blind. Keine Sorge: darauf wollen wir hier und heute nicht weiter eingehen.

Allerdings hält Bolle es für angebracht, darauf hinzuweisen, daß Mathematik ohne Sinn durchaus hohl ist. Unser Bildchen zeigt in der ersten Zeile eine Funktion in ihrer Normalform y = f (x). Der Wert einer Zahl y hängt also davon ab, welchen Wert eine andere Zahl x jeweils annimmt – und nur davon. Wie hängt sie davon ab? Nun, wer öfters mal mit sowas zu tun hat, sieht, daß es sich um eine Logarithmusfunktion handelt – egal, was das denn schon wieder sein soll – und daß da noch verschiedene Parameter m, s, a und r im Spiel sind. Für was genau diese Parameter – Zahlen, die innerhalb einer gegebenen Aufgabe unveränderlich sind – stehen mögen, spielt im Moment keine Rolle.

Kurzum: die erste Zeile zeigt einen Zusammenhang auf, der uns – beziehungsweise niemandem: auch keinem Mathematiker – irgend etwas zu sagen vermag, solange wir nicht wissen, wofür die Parameter stehen und was sie bedeuten sollen. Kurzum, zum zweiten: wir müssen interpretieren. Dabei versteht man in Bolles Kreisen unter ›interpretieren‹ im Grunde nicht mehr als die ›Beimessung von Bedeutung‹. Was dabei für wen Bedeutung haben mag, steht wiederum auf einem ganz anderen Blatt.

In unserem Bildchen ist es so, daß durch vier einfache Umformungen, die mathematisch (bis auf ganze Kleinigkeiten) nicht zu beanstanden sind – Bolle hat nachgerechnet – eine Gleichung herauskommt, die an einen gebräuchlichen Weihnachtsgruß erinnert. Und schon haben wir Bedeutung! – und zwar in diesem Falle, ohne daß wir wissen müßten, wofür die Parameter stehen oder was es mit einer Logarithmusfunktion auf sich haben mag.

Kurzum: Mathematik ohne Sinn – also ohne hineininterpretierbare Bedeutung – ist hohl, und sagt nichts, wirklich rein gar nichts, aus. Da hilft es auch nicht zu lamentieren, das aber seien schließlich die „Fakten“. Das stimmt zwar – nützt aber nichts. Oder, um es – etwas kryptisch zwar, das sieht Bolle ein, aber bitteschön – mit einem Epigramm aus Bolles Sammlung ewiger Wahrheiten zu sagen:

Wenn der Kant kackt
auf dem Klo,
ist er nackt
rund um den Po.

Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

17-12-202517-12-2025

Mi 17-12-25 Das siebzehnte Türchen: Wenn Gansl ganz schnell garen

Hurtig, hurtig, tralaralala! (Symbolbild, of course).

Weihnachten steht vor der Tür. Falls Bolle sich nicht verrechnet hat, ist das gerade mal noch genau eine Woche hin. Höchste Zeit also, mit praktischen Tipps aus unserer Abteilung ›Schneller kochen‹ aufzuwarten. Neben ›easy cooking‹, das sich in Bolles überwiegend minimalistisch ausgerichteten Kreisen ja einer gewissen Beliebtheit erfreut, sollte nämlich auch selbiges mitnichten zu kurz kommen.

Stellen wir uns das folgende Szenario vor. Heiligabend steht unmittelbar vor der Tür. Zum Feste soll es – das hat die Hausfrau (beider- bzw. allerlei Geschlechts, of course) so beschlossen – Gansl geben. Der Weihnachtsschmaus ist für 20 Uhr geplant. Jetzt ist es 17 Uhr. Zwar ist die Gans schon aufgetaut und auch gefüllt mit Apfel, Nuß und Mandelkern. Allein sie ist noch – man darf das sagen, ohne übermäßig roh zu wirken – in einer ebensolchen Verfassung.

Um pünktlich zum Feste duftend auf dem Weihnachtstisch zu stehen, bleiben dem Gansl also noch drei Stunden. Das Rezept, und auch die Erfahrung, sagen aber, daß es eher vier Stunden brauchen wird, um zu duftender weihnachtlicher Hochform aufzulaufen. Was tun?

Nun – wenn das Gansl bei 200° C vier Stunden braucht, dann wird es bei 300° C wohl nur zwei Stunden und vierzig Minuten brauchen. Damit blieben also noch zwanzig Minuten zum Anrichten und zum Wein einschenken – etwa einen Spätburgunder beziehungsweise, wer’s lieber auf Französisch mag, einen Pinot Noir.

Bei der Berechnung handelt es sich übrigens um elementaren Dreisatz, of course: Wenn die Temperatur drei Halbe mal so hoch ist wie im Rezept, dann sollte die Gare nur zwei Drittel der veranschlagten Zeit betragen. Derlei läßt sich mit jedem handelsüblichen Taschenrechner – der bei dieser Methode allerdings in keiner Küche fehlen sollte – in wenigen Sekunden leicht berechnen.

Das ist wahrlich keine Hexerei. Vielmehr verhält es sich ganz ähnlich wie mit Professor Eberbachs (dem aus Spoerls Feuerzangenbowle) Matheaufgaben: Jemand wirft einen zwei Pfund schweren Stein dreiundzwanzig Meter weit. Wie weit würde er einen Stein von 0,3 Gramm werfen? Alles schon mal dagewesen, also.

Bolle für sein Teil – das zu erwähnen gebietet die Redlichkeit – ist von der Schneller-kochen-Methode noch nicht ganz restlos überzeugt. Das mag an seiner skeptischen Grundhaltung liegen – vielleicht aber auch an der Methode. Da gibt’s nur eines: probieren geht über studieren! Bolle würde als geeigneten Termin für ein solches Experiment allerdings nicht unbedingt den 24. Dezember wählen. Im übrigen bleibt er traditionell und easy-cooking-mäßig ja ohnehin lieber bei Hölzerbrot (vgl. etwa Sa 07-12-24 Das 7. Türchen: Wollense Toast …?). Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

29-06-202529-06-2025

So 29-06-25 Rechtes Rechnen

Es ist noch gar nicht allzu lange her, da ging es uns um die Kunst vorausschauenden Fahrens nebst der Unmöglichkeit, es in selbiger zur Meisterschaft (beider- bzw. allerlei Geschlechts, of course) zu bringen, wenn es einem an Scharfsicht gebricht (vgl. dazu So 27-10-24 Vorausschauend fahren! Können vor Lachen). Unser Fazit seinerzeit: Wer kurzsichtig ist – und sei es auch nur leicht – tut gut daran, selbiges zur Kenntnis zu nehmen und keine Karriere zum Beispiel als Rennfahrer anzustreben. Er wäre stets nur zweite Wahl – und auf die Dauer gar nicht glücklich.

Damals meinte Bolle, faustgestählt, in Anbetracht einer Rüge seines Fahrlehrers, das Schild da säh‘ er wohl, allein er könnt‘s nicht lesen – jedenfalls nicht auf die Entfernung. Damit hatte die Angelegenheit ihr Bewenden. Bolle hat seine Führerscheinprüfung anstandslos im ersten Anlauf bestanden, of course.

Was aber wäre gewesen, wenn Bolle anders reagiert hätte, etwa wie folgt: ›Schilder? Regeln überhaupt? Interessieren mich nicht.‹ Man nennt das wohl ›Aus der Not (der Kurzsichtigkeit) eine Tugend machen‹. Zugegeben, das klingt erst mal schrill. Allein, wenn man sich umguckt auf der Welt, scheint diese Masche, zumindest bei einigen Leuten, einigermaßen en vogue zu sein. Und, wie’s weiterhin scheint, durchaus auch mit gewissem Erfolg. Hier ein Beispiel, wie es Bolle vor Kurzem erst untergekommen ist.

Ein Mathelehrer wollte seine gymnasiale Oberstufe lehrplanmäßig mit der Familie der e-Funktionen vertraut machen. Als Anschauungsmaterial wählte er zwei Populationen – nennen wir sie Ping und Pong. Dabei ist Ping (rötliche Kurve) im Ausgangspunkt (auf der x-Achse Null) dreimal so stark wie Pong (blaue Kurve). Allerdings, so das Beispiel, vermehre sich Pong mit 3 Prozent jährlich, Ping dagegen nur mit 1 Prozent – also nur ein Drittel so sehr. Die zu lösende Aufgabe: Wie lange wird es dauern, bis Pong genauso stark ist wie Ping – und wie geht es dann weiter?

Nun, auch ohne uns mit der Familie der e-Funktionen vertraut machen zu müssen: Aus der Graphik läßt sich leicht ablesen, daß das schon nach 55 Jahren der Fall sein wird. Ab da schießt Pong (die blaue Kurve) buchstäblich durch die Decke. Und zwar so lange, wie sich an den Wachstumsraten nichts ändert.

Wie ging es weiter mit der Geschichte? Statt zu sagen: ›Potzblitz! Was sich alles rechnen läßt! Das ist ja interessant!‹ hieß es in Teilen der besorgten Elternschaft, das sei ja wohl sowas von rechter, wenn nicht gar rechtsextremer Mathematik. Unklugerweise nämlich hatte unser Mathelehrer die Aufgabe nicht an Ping und Pong, sondern an Einheimischen versus Zugereisten aufgezogen. Eine Zumutung! So etwas habe an einer höheren Lehranstalt natürlich nichts verloren. Der Lehrer müsse möglichst umgehend entlassen werden. Weg, weg, weg! Die armen Kinder! – und so weiter, und so fort.

Bolle sieht hier eine äußerst beunruhigende Parallele zu seiner fiktiven ›Was interessieren mich Regeln‹-Replik. Auch Regeln der Mathematik haben gefälligst politisch korrekt zu sein. Da sind Teile der Elternschaft offenbar selber nicht in der Lage zu rechnen – zumindest tun sie es nicht. Und wenn ihnen dann einer die Rechnung auf die sprichwörtliche Nase bindet, fühlen sie sich mitnichten bereichert – Heureka! – sondern in ihrem woken Weltbild aufgewühlt.

Und? Was macht der Journalismus 2.0 …? Stets auf der Suche nach Sensationen stürzt er sich mit Schwunge drauf – und bestärkt die Paragonisten damit in ihrer gerechten Empörung. Bolle meint, vermutlich kennt man dort die e-Funktionen ohnehin auch nur vom Hörensagen.

Natürlich ist das Phänomen an sich nicht neu. 1976 schon sahen sich Politikdidaktiker (welch ein Wort, by the way) veranlaßt, sich als Handreichung für das Lehrpersonal auf einen Beutelsbacher Konsensus mit drei Punkten zu verständigen. Erstens das sogenannte Überwältigungsverbot: Keinem Schüler soll eine Meinung aufgezwungen werden. Allerdings, meint Bolle, kann es durchaus passieren, daß sich der eine oder andere Schüler (beider- bzw. allerlei Geschlechts, of course) gleichwohl von Mathe überwältigt fühlt. Zweitens das Kontroversitätsgebot: Was strittig ist, soll strittig bleiben. Ziel ist auch hier die freie Meinungsbildung. Allerdings findet Bolle, daß das ja wohl ein wenig aus der Zeit gefallen sei. ›Eine Meinung muß genügen: mehr hältste ja im Kopp nich aus‹ – und verweist dabei gerne auf Hauke Arachs ›Mensch, lern das und frag nicht‹ aus dem Jahre 2013 (vgl. dazu etwa So 22-09-24 Opinio et Reactio). Seitdem ist diesbezüglich ja wohl so einiges den Beutelsbach runtergegangen – um mal ein wenig zu kalauern. Der dritte Punkt? Spielt hier keine Rolle.

Ist das jetzt alles übertrieben? Vermutlich leider nicht. Kaum einer kann rechnen – und falls doch, will es niemand wahrhaben. Immerhin würde das umstandslos so manch maroden Zustand im Lande erklären: von Schulen, Straßen und auch Schwimmbädern – bis hin zum vielbeklagten „jahrzehntelangen Investitionsstau“ überhaupt. Anscheinend aber kommt kaum einer auf die Idee, sich zu fragen, wie das alles überhaupt jemals so weit kommen konnte. Stattdessen scheißt man die Probleme lieber mit einem Riesenhaufen Knete zu – ganz nach dem Motto ›Was interessieren mich Regeln? Was interessiert mich Rechnen? Was Mathematik?‹. Kann man so machen – wenn auch vermutlich nicht auf Dauer. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

08-06-202505-10-2026

So 08-06-25 Wenn Glocken richtig rocken

Nach den doch eher etwas fluffigeren Sujets der letzten Sonntagsfrühstückchen wollen wir uns diesmal wieder einem strikteren Gegenstand zuwenden. Kenner werden es sogleich erkannt haben: Wir reden hier von der Gauß’schen Glockenkurve. Ersonnen hat sie Carl Friedrich Gauß (1777–1855), der zu Lebzeiten schon als Princeps mathematicorum, also Erster seiner Zunft galt, seinerzeit im Jahre 1809.

Was will uns Gauß damit sagen?

Stellen wir uns ein Weizenfeld vor (etwaige Allergiker, beider- bzw. allerlei Geschlechts, of course, mögen sich mit einem Dinkelfeld begnügen). Nehmen wir an, die Halme seien im Mittel 100 cm hoch (in der Graphik entspricht das der 0) und hätten eine sogenannte Standardabweichung von ±10 cm (in der Graphik entspricht das dem Bereich zwischen –1 und +1). Das bedeutet, daß wir erwarten können, daß 2/3 der geernteten Halme zwischen 90 und 110 cm lang sein werden und damit „Mittelmaß“. Natürlich werden sich auch Halme finden, die zwischen 110 cm und 120 cm hoch sein werden. Allerdings, das sagt uns die Glockenkurve, wird das nur rund 1/7 der Halme sein. Noch größer als 120 cm – auch das kommt vor – werden nur noch 1/42, also knapp 2,5% der Halme sein (in der Graphik das Feld ›top‹). Das Gegenstück ›ui‹ übrigens steht für ›unterirdisch‹ – obwohl das, zugegebenermaßen, bei Halmlängen ein schiefes Bild ergibt. Oder – auch das sagt die Graphik aus – um zum oberen Drittel zu gehören, müßte ein Halm wenigstens gut 104 cm lang sein (rote Linie). Damit wäre er zwar immer noch Mittelmaß – allerdings schon leicht überdurchschnittlich.

Wer nun meint, was interessieren mich Weizen- oder Dinkelfelder? Mehl kommt mir aus der Tüte beziehungsweise Brot gibt’s beim Bäcker – dem sei gesagt, daß sich die Gauß’sche Glockenkurve auf erstaunlich viele Bereiche im wirklichen Leben anwenden läßt – unter anderem auf so weizenferne Felder wie Leistungsfähigkeit und -bereitschaft (also etwa Schulnoten, wenn sie denn gerecht vergeben würden) oder eben auch auf das, was wir hier politische Urteilskraft nennen wollen.

Übertragen bedeutet das: Unter den Bedingungen einer Demokratie werden Leute mit guter oder sehr guter politischer Urteilskraft schwerlich regieren können – einfach, weil sie nicht in der Mehrheit sind. Selbst für eine sogenannte Sperrminorität (rote Linie) wird es absehbar eng, weil es dafür nötig wäre, einen gehörigen Teil des Mittelmaßes zu gewinnen. Die Vorzüge einer Demokratie können also nur woanders liegen. In der Gauß’schen Glockenkurve jedenfalls liegen sie nicht.

Was aber soll das überhaupt sein, politische Urteilskraft? Die einfachste und ganz naheliegende Antwort wäre wohl: Politische Urteilskraft hat in meinen Augen, wer die Partei wählt, die ich selber auch wählen würde. Easy – aber führt zu nichts. Drehen wir den Spieß also um: Was würde nahelegen, daß es einem (beider- bzw. allerlei Geschlechts, of course) an selbiger mangelt? Im Wesentlichen wohl, daß er nicht wirklich in der Lage ist, sich ein Bild zu machen von den jeweiligen Paragonisten (neudeutsch: Akteuren) oder Gegebenheiten. Da bricht einer alle Wahlversprechen, gelobt kurz vor der Wahl Besserung – er habe es schließlich nicht besser wissen können – und wirbt treuherzig um „Vertrauen“. Und die Leute wählen ihn wieder. Da werden im Vorfeld einer Wahl regelmäßig regelrechte Plakatschlachten veranstaltet – und mancher Wähler läßt sich, wie’s scheint, davon dann doch irgendwie beeindrucken. Da postet einer schicke Reels auf Insta – und kriegt dafür (!) die Stimme. Da gibt es Last-Minute-Wähler, die zehn Minuten vor der Stimmabgabe noch immer nicht wissen, was sie wählen wollen – als hätten sie nicht Monate und Jahre Zeit gehabt, sich ein solides Bild zu machen und zu einem fundierten politischen Urteil zu kommen. Schließlich gibt es auch noch Wähler, die wählen sowieso immer, was sie schon immer gewählt haben – egal, was auch immer die Paragonisten veranstalten mögen: Traditionales Verhalten, halt. Kurzum: Mangelnde politische Urteilskraft scheint ein Spezialfall von mangelnder prognostischer Kompetenz zu sein: Die Unfähigkeit zu erahnen, was passieren wird, wenn dieses oder jenes so weitergeht. Kognitive Kurzsichtigkeit also. Oder, wie Bolle das womöglich resümieren würde:

Kurzum –
Und dabei völlig ohne Hohn:
Ein klitzekleines bißchen dumm
Wirkt das alles dann doch schon.

Und so sucht, entgegen dem völlig anderslautenden Paratickma, auch kein Aas das angeblich bessere Argument, sondern lediglich die bessere Agitation. Auch hier scheint, einmal mehr, ›Luhmanns Law‹ zu gelten. In Bolles Fassung lautet es (vgl. dazu Mo 12-12-22 Das zwölfte Türchen …):

Das System erzeugt die Elemente,
aus denen es besteht,
mittels der Elemente,
aus denen es besteht.

Wir haben es hier also wohl einfach nur mit zielgruppengerechter Ansprache zu tun – wobei die Zielgruppe das Mittelfeld ist, also der Bereich zwischen –1 und +1. Und die Medien mischen munter mit. Daher womöglich auch der geradezu heilige Zorn gegen alles, was sich davon nicht einfangen lassen will, geschweige denn unterhaken – und damit das Idyll einer Schönwetter-Demokratie trübt. Im Überschwange geht das dann so weit, daß manche ernstlich meinen, Einigkeit sei eine demokratische (!) Tugend. Hört, hört! Mit derlei wird man leben müssen – und gegebenenfalls auch leiden. Abhilfe ist nicht in Sicht – und zwar aus rein mathematischen Gründen nicht. Was aber rein mathematisch nicht funktioniert, kann auch in der besten aller möglichen Welten (Voltaire 1759) nicht funktionieren. Eine damit oft verbundene regelrechte ideologische Überhöhung aber – 🎶 Im Westen, im Westen, da ist‘s ja wohl am besten, Fidirallala, … 🎶 – können wir getrost den Hülsenfrüchtchen überlassen.

Eines aber wollen wir dabei – Bolle featuring Marx/Engels 1848 – nicht vergessen: Die Parlamentarier haben nichts zu verlieren als ihre Buletten. Sie haben ihre Welt zu gewinnen. Parlamentarier aller Länder, vereinigt Euch! – namentlich gegen Wahlvolk mit mittelmäßiger politischer Urteilskraft. Das aber ist dann doch schon wieder ein ganz anderes Kapitel.

14-12-202414-12-2024

Sa 14-12-24 Das 14. Türchen: Schneemann, Teppich, Meilenstein

Zu unserem Türchen gestern gab es eine Rückmeldung: „Wieso? Das sieht man doch, ob sich der Schneemann bewegt hat oder der Teppich.“ Da wir hier, wie gestern erläutert, eine wohlverstandene relativistische Perspektive einnehmen wollen, scheint uns ein kleiner Nachtrag angebracht.

Natürlich sieht man das. Aber warum sieht man es? Weil wir – ohne uns dessen bewußt zu sein – das Blatt Papier beziehungsweise den Bildschirmausschnitt als Bezugspunkt verwenden. Einen solchen Bezugspunkt haben wir aber nicht – nicht in der Physik und erst recht nicht im wirklichen bzw. sozialen bzw. politischen Leben. Dieses völlige Fehlen eines Bezugspunktes hat übrigens die Physiker ziemlich lange Zeit ziemlich rappelig gemacht und zu so mancher Idee inspiriert, die sich letztlich als nicht soo brauchbar erwiesen hat. So etwas ist aber auch jeglicher Alltagserfahrung allzu ferne. Wir sind nun mal seit sechs Millionen Jahren – also seit der Menschwerdung im weiteren Sinne – daran gewöhnt, daß es feste Bezugspunkte gibt. Entsprechend schwer fällt es uns, sich die einfach wegzudenken – auch wenn sie wirklich mal nicht da sein sollten.

Um uns das alles besser vorstellen zu können, hilft ein kleiner Trick: Nehmen wir an, das Blatt Papier oder der Bildschirmausschnitt, auf dem sich Schneemann und Teppich befinden, sei unendlich groß – zumindest aber unüberschaubar groß. Dann gibt es wirklich keine Möglichkeit, das eine vom anderen zu unterscheiden. Oder aber wir fügen, tout au contraire, einen Meilenstein in die Graphik ein – eine Wegmarke, an der wir uns orientieren können. Unter der Annahme, daß sich Schneemann und Teppich im Freien befinden – wer stellt sich schon einen Schneemann ins Wohnzimmer? – könnte das irgendein markanter Punkt in der Landschaft sein, zum Beispiel ein Baum oder Busch oder ähnliches (siehe Bildchen). Relativ zu dieser Wegmarke können wir nun eindeutig entscheiden, wer oder was sich bewegt hat – Schneemann oder Teppich?

Jetzt – aber erst jetzt – denken wir uns die Wegmarke wieder weg. Im Grunde wenden wir also die Vorgehensweise von Professor Bömmel aus der Feuerzangenbowle an: „Also, wat is en Dampfmaschin? Da stelle mehr uns janz dumm.“

In der sozialen beziehungsweise politischen Sphäre kommt allerdings erschwerend hinzu, daß es bereits an der Definition hapert: kein Mensch kann zufriedenstellend erklären, was genau das eigentlich sein soll: lechts oder rinks? (Ernst Jandl 1966). Bolle, stets bemüht, auch das Unfaßbare wenigstens anekdotisch faßbar zu machen, hält sich immer an die folgende Faustregel …

Motto „rechts“: Bevor Du dich daran machst, die Welt zu verbessern, kehre drei mal vor Deiner eigenen Tür (chinesisches Sprichwort).
Motto „links“: Wieso? Alles und jeder braucht unsere Solidarität. Immer!

… und muß dabei stante pede an Churchill denken, of course, der angeblich mal gesagt haben soll:

Wie herrlich Deine Strategie auch sein mag:
Gelegentlich solltest Du gucken, was dabei rauskommt.
(However beautiful the strategy,
you should occasionally look at the results.)

Das alles aber ist dann doch schon wieder ein ganz anderes Kapitel.